【正确答案：A】

设M（x，y，z）为曲线p上任一点，则点M处的切向量为：l=（-asint，acost，b），而z轴的方向向量为k=0，0，1，于是l与k的夹角为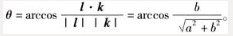：故该曲线上任一点处的切线与z轴成定角θ。

【正确答案：C】

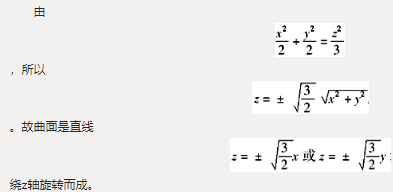
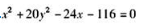
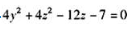
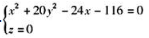
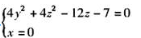
【正确答案：A】

由②得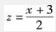，代入①化简得：为L在xOy面上的投影柱面方程。而C项为投影的曲线方程。

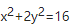
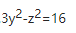
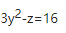
【正确答案：C】

因柱面的母线平行于x轴，故其准线在yOz平面上，且为曲线在yOz平面上的投影，在方程组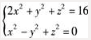中消去x得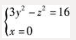：，此即为柱面的准线，故柱面的方程为：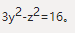

【正确答案：C】

即求曲面S：F（x，y，z）=0，其中F（x，y，z）=z+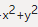-4上点P使S在该点处的法向量n与平面π：2x+2y+z-1=0的法向量n0=2，2，1平行。

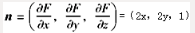
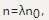S在P（x，y，z）处的法向量λ为常数，即2x=2λ，2y=2λ，1=λ。即x=1，y=1，又点P（x，y，z）∈S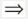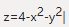（x，y）=（1，1）=2，求得P（1，1，2）（P不在给定的平面上）。

【正确答案：D】

设过点P（1，0，1）的直线L分别与直线L1、L2交于点A和点B，由L1和L2的方程知可设点A的坐标为（λ，λ-1，-1），存在常数μ使点B的坐标为（1+μ，2，3+μ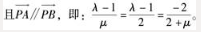），由此可求得λ=0，μ=2，即点A为（0，-1，-1），点B为（3，2，5）。从而，直线L的方向向量可取任一平行于的非零向量。

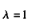
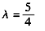
【正确答案：D】

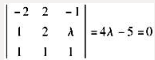如果两直线相交，则这两条直线的方向向量与这两条直线上两点连线构成的向量应在同一平面上，由此来确定λ。点A（1，-1，1），B（-1，1，0）分别为两条直线上的一点，则，两条直线的方向向量分别为s1=（1，2，λ），s2=（1，1，1），这三个向量应在同一个平面上，即：，解得：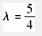

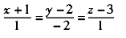
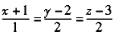
【正确答案：A】

直线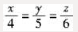的方向向量为s=4，5，6，平面7x+8y+9z+10=0的法向量为n=7，8，9。显然A、B、C中的直线均过点（-1，2，3）。对于A中直线的方向向量为s1=1，-2，1，有s1⊥s，s1⊥n，可见A中直线与已知直线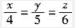垂直，与平面7x+8y+9z+10=0平行。

【正确答案：C】

直线L的方向向量为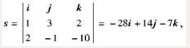： 即s={-28，14，-7}。平面π的法线向量为：n={4，-2，1}。由上可得，s、n坐标成比例，即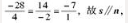

直线L垂直于平面π。

【正确答案：A】

因点（-1，2，-3）不在平面x+z=0上，故可排除B项；因点（3，-1，1）不在x-2y+z=0和x+y+z=1这两个平面上，故可排除CD两项，选A项。由于题目所给两条直线的方向向量相同，故为两条平行直线，且已知两个点分别为（-1，2，-3）和（3，-1，1），过这两个已知点的直线方程的方向向量为：（4，-3，4），故可求得通过这三条直线（两条平行线和一条与平行线相交的直线）平面的法向量为：