- 问题求解下列各项表述中正确的是（）。
- A 、两个无理数的和是无理数
- B 、两个无理数的乘积是无理数
- C 、两个无理数的乘积是有理数
- D 、-个有理数和一个无理数的乘积是无理数
- E 、一个有理数和一个无理数相加减，其结果是无理数
扫码下载亿题库
精准题库快速提分
参考答案【正确答案：E】
两个无理数的和或差不一定是无理数。例如，
，则a+b=4是有理数；
两个无理数的乘积或商不一定是无理数，例如，
，则
是有理数，若
，则
是无理数，因此A，B，C都不正确.
一个有理数和一个无理数的乘积可能是有理数，也可能是无理数，例如，
，则ab=0是有理数，若a≠0，a为有理数，b为无理数，则ab一定是无理数，因此D不正确，
一个有理数和一个无理数相加减，其结果一定是无理数。即E是正确的.
您可能感兴趣的试题- 1 【问题求解】下面结论正确的是（）。
- A 、两个有理数的和为正数时，这两个数都是正数
- B 、两个有理数的和为负数时，这两个数都是负数
- C 、两个有理数的和一定大于其中一个加数
- D 、两个有理数的和可能等于零
- E 、两个有理数的商不一定是有理数（除数不为0）
- 2 【问题求解】已知数列
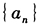的前n项和
，则下面正确的是（）。 - A 、
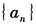是等差数列 - B 、
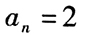
- C 、
- D 、
- E 、以上均不正确
- 3 【条件充分性判断】各项均为正数的等比数列
的前n项和为
=30。（） （1）
（2）
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 4 【问题求解】下面命题正确的是（）。
- A 、有两边和一角对应相等的两个三角形全等
- B 、有一边对应相等的两个等边三角形全等
- C 、有一角对应相等的两个等边三角形全等
- D 、有一角对应相等的两个直角三角形全等
- E 、以上结论均不正确
- 5 【问题求解】已知各项均为正数的等比数列
中，
，
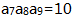，则
（）。 - A 、
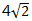
- B 、7
- C 、6
- D 、
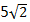
- E 、
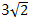
- 6 【条件充分性判断】已知等比数列
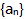的各项都是正数，则表达式
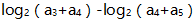的值为-2。（） （1）
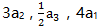成等差数列 （2）
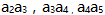成等比数列 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 7 【条件充分性判断】已知等比数列
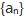的各项都是正数，则表达式
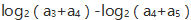的值为-2。（） （1）
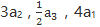成等差数列 （2）
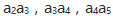成等比数列 - A 、条件（1）充分，但条件（2）不充分
- B 、 条件（2）充分，但条件（1）不充分
- C 、 条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和（2）联合起来也不充分
- 8 【论说文】分析下述材料，准确审题立意。 古时候，有一位伟大的品酒师。一天，一个朋友邀请品酒师去家里，因为他有一些好酒，想让品酒师看看他的收藏。为了得到品酒师的赞赏，他首先拿出一种最名贵的酒。品酒师品尝了一下，结果却没有发表任何赞誉之词。 主人又拿出了一种非常普通的酒。品酒师品尝了一下，说：“好酒！好酒！” 主人这下子糊涂了，他说：“我真不知道，为什么你对真正的好酒保持沉默，但对这种普通的酒却大加赞扬呢？” 品酒师思索了一会儿，然后说：“我之所以不赞扬真正的好酒，而要赞扬普通的酒，是因为……”
- 9 【论说文】分析下述材料，准确审题立意。 拳王阿里33岁那年与挑战者弗雷泽进行第3次较量。在进行到第14回合时，阿里已筋疲力尽，几乎再无丝毫力气迎战第15回合了。然而他拼命坚持着，因为他心里知道，对方肯定和自己一样，如果在精神上压倒对方，就有胜出的可能。于是他竭力保持坚毅的表情和永不低头的气势，双目如电，令弗雷泽不寒而栗，以为阿里还存有旺盛的体力，阿里的教练发现弗雷泽已有放弃的念头，便使眼色暗示阿里。阿里精神一振，更加顽强地坚持着，果然在关键时刻，对手认输了。卫冕成功的阿里还未走到擂台中央，便眼前一黑，双腿无力地跪倒在地上。弗雷泽见此情景，如遭雷击，并为此抱憾终生。
- 10 【论说文】分析下述材料，准确审题立意。 有一老一小两个人同时在沙漠里种胡杨树。年轻人待树苗成活以后，每隔三天就要来给它浇水，而老人一等到树苗成活以后，就来得很少；即使来了，也只是把被风刮倒的树苗扶一扶，不浇一点水。转眼几年过去了，胡杨树都长得很粗了。忽然有一天刮起了沙尘暴，第二天风停后，两人惊讶地发现，年轻人种的胡杨几乎全被风刮倒了，有的甚至连根拔起；而老人种的树，只是被风吹折了一些树枝，吹掉了一些树叶。年轻人很诧异，问起原因，老人道：“你经常给树浇水施肥，它的根就不往泥土深处扎。如把树栽活以后就不去理睬它，就逼得它们不得不把自己的根一直扎到地底下的泉源中去。有这么深的根，这些树怎能轻易被风刮倒？”
热门试题换一换
- 分析下述论证中存在的缺陷和漏洞，选择若干要点，写一篇600字左右的文章，对该论证的有效性进行分析和评论。（论证有效性分析的一般要点是：概念特别是核心概念的界定和使用是否准确并前后一致，有无各种明显的逻辑错误，论证的论据是否成立并支持结论，结论成立的条件是否充分等等。） “赢家诅咒”是一个经济学，也是行为金融学的概念。最近，我一直在想，它会不会就要在中国楼市发生。 赢家诅咒的情形，主要发生在竞拍之中。拍卖时，市场只有一个卖家，但买家有很多。比如，古董、字画等艺术品，都会采取这种拍卖模式。 买家在竞买的过程中，需要不断加价，最后是出价最高者得。但是，从常识来看，这样不断的买家“恶性竞争式”加价，会把一个拍卖品的价格抬得过高，大幅超越其本来应有的价值。那么，最后付了巨资，拿到这个拍卖品的人可能会暗自后悔。 他拿到了那个拍卖品，是现场万众瞩目的人生赢家，但得到的却是一个“价值次品”——这些古人用过的瓶瓶罐罐或信手涂鸦根本就不值这个价。这就是赢家诅咒。 从理论上讲，中国的房地产商和购房者都是有着赢家诅咒风险的一群人。房地产商拿地，是竞拍的，卖家只有一个，即当地政府，而很多个买家竞价。最后，楼面价不断被刷新。 对购房者而言，由于这个市场严重的信息不对称，所以，中介和房东（或者说先入楼市者）坐地起价、临时加价的现象司空见惯。实际上，前段时间，某些城市的学区房抢购大战，已经有点类似于拍卖了。真是天下奇观。 不过，由于中国楼市，特别是一线城市“永远涨”的预期，帮助面临赢家诅咒的地产商和购房者似乎破除了这个“诅咒”。因为，还有更高的出价者来接盘。“离婚购房”、“贷款千万购房”的人，是否就是这么想的？ 但是，这样的想法也许恰好就是即将崩盘的中国楼市“赢家诅咒”出现的前兆？
- I decided to go to the library as soon as I( ).
- 2000年，宏发投资基金的基金总值40%用于债券的购买。近几年来，由于股市比较低迷，该投资基金更加重视投资债券，在2004年，其投资基金的60%都用于购买债券。因此，认为该投资基金购买债券比过去减少的观点是站不住脚的。 以下哪项如果为真，最能削弱上述论证（）。
- 鸽子走路时，头部并不是有规律地前后移动，而是一直在往前伸。行走时，鸽子脖子往前一探，然后，头部保持静止，等待着身体和爪子跟进。有学者曾就鸽子走路时伸脖子的现象做出假设：在等待身体跟进的时候，暂时停止的头部有利于鸽子获得稳定的视野，看清周围的事物。 以下哪项如果为真，最能支持上述假设（）。
- The following sentence（）isright.
- 设长方体的三条棱长分别为a，b，c，若其所有棱长之和为24，对角线的长度为5，体积为2，则为（）。
- 天南大学准备派两名研究生、三名本科生到山村小学支教。经过个人报名和民主决议，最终人选将在研究生赵婷、唐玲和殷倩等3人和本科生周艳、李环、文琴、徐昂、朱敏等5人中产生。按规定同一学院或者同一社团至多选派一人。已知： （1）唐玲和朱敏均来自数学学院； （2）周艳和徐昂均来自文学院； （3）李环和朱敏均来自辩论协会。 根据上述条件，以下必定入选的是（）。
- 若 （）。
- 自然数n的各位数字之积为6。（） （1）n是除以5余3，且除以7余2的最小自然数 （2）n是形如（m是正整数）的最小自然数
- Foodshortage become more serious in
亿题库—让考试变得更简单
已有600万用户下载
PWrGY