- 问题求解圆柱体的侧面积扩大到原来的8倍，高扩大到原来的2倍，则底面半径扩大到原来的倍数是（）。
- A 、2
- B 、4
- C 、8
- D 、
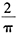
- E 、
扫码下载亿题库
精准题库快速提分
参考答案【正确答案：B】
设原来圆柱体的底面半径为r，高为h，侧面积为S，扩大后的底面半径为
，则由题意
您可能感兴趣的试题- 1 【条件充分性判断】 圆柱体的侧面积是32π。（） （1）圆柱体的高与底面直径相等 （2）圆柱体轴截面的面积为32
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 2 【条件充分性判断】长与宽之比为2：1的矩形的面积增大为原来的2倍。（） （1）宽增大，长不变，使之成为正方形 （2）宽增大为原来的2倍，长缩小为原来的一半
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 3 【问题求解】圆的半径缩小到原来的
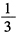，那么原来的面积是缩小后的面积的（）。 - A 、3倍
- B 、6倍
- C 、9倍
- D 、10倍
- E 、12倍
- 4 【条件充分性判断】圆的面积增大到原来的9倍。（） （1）圆的半径增大到原来的3倍 （2）圆的周长增大到原来的3倍
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 5 【问题求解】立方体的边长扩大为原来的2倍后，体积比原来的体积大多少倍？（）
- A 、5
- B 、6
- C 、7
- D 、8
- E 、9
- 6 【问题求解】圆柱体的底面积为1，侧面展开图是—个正方形，则其侧面积与底面积的比是（）。
- A 、4π
- B 、2π
- C 、π
- D 、
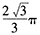
- E 、
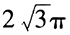
- 7 【问题求解】球的体积增大到原来的27倍，则其表面积扩大了（）。
- A 、3倍
- B 、10倍
- C 、9倍
- D 、8倍
- E 、7倍
- 8 【条件充分性判断】两圆柱体的侧面积相等，则能求出它们体积之比为3：2。（） （1）它们的底面半径分别是6和4 （2）它们的底面半径分别是3和2
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 9 【条件充分性判断】圆柱体积是正方体体积的
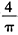倍。（） （1）圆柱的高与正方体的高相等 （2）圆柱的侧面积与正方体的侧面积相等 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 10 【问题求解】 一圆柱体的高与一正方体的高相等，且它们的侧面积也相等，则圆柱体的体积与正方体体积的比值为（）。
- A 、π/4
- B 、4/3
- C 、4/π
- D 、3/4
- E 、3/5
热门试题换一换
- His grandmother( )for twenty years.
- Com originated in the New World and thus was not known in Europe until Columbus found it( )in Cuba.
- 新挤出的牛奶中含有溶菌酶等抗菌活性成分。将一杯原料奶置于微波炉加热至50℃，其溶菌酶活性降低至加热前的50％。但是，如果用传统热源加热原料奶至50℃，其中的溶菌酶活性几乎与加热前一样，因此，对酶产生失活作用的不是加热，而是产生热量的微波。 以下哪项如果属实，最能削弱上述论述（）。
- Writea letter of about 100 words to your American friend Jam, recommending yourChinese friend Han Ling to teach him Chinese. You should include the details you think necessary. You should write neatly on the ANSWER SHEET. Do not use your own name. Use "Li Ming" instead. Do not write the address.
- 设x是非零实数，则。（） （1） （2）
- n为任意正整数，则 必有约数（因数）（）。
- 若甲不排前排，有多少种不同的排法？
- （8）
亿题库—让考试变得更简单
已有600万用户下载
mOMj1