- 条件充分性判断
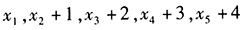的算术平均值是
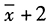（） （1）如果
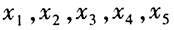的算术平均值是
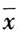（2）如果
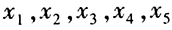的算术平均值是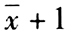
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
扫码下载亿题库
精准题库快速提分
参考答案【正确答案：A】
由条件（1）
，则
，从而
，即条件（1）是充分的。
由条件（2）
，则
，即条件（2）不充分。
您可能感兴趣的试题- 1 【条件充分性判断】 M=60。（） （1）若
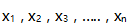的算术平均值为
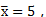方差
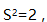则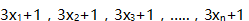
的算术平均值与方差之和为M （2）现从一组生产数据中，随机抽取五个样本7,8,9,x,y的算术平均值是8，标准差是
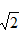，则xy的值为M - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和（2）联合起来也不充分
- 2 【问题求解】等差数列
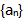中，a1=-5，前11项的算数平均值是5，从中抽取一项，余下10项的平均值是4，则抽取的项是第（）。 - A 、7项
- B 、10项
- C 、11项
- D 、8项
- E 、9项
- 3 【问题求解】若实数a，b，c的算术均值为13，且
，那么c= （）。 - A 、7
- B 、8
- C 、9
- D 、12
- E 、18
- 4 【条件充分性判断】已知
为实数，
为
的平均值，则
。（） （1）
（2）
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 5 【问题求解】如果
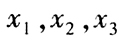三个数的算术平均值为5，则
与8的算术平均值为（）。 - A 、
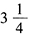
- B 、
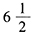
- C 、7
- D 、
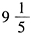
- E 、以上结论均不正确
- 6 【简答题】求3，8，9这三个数的算术平均值和几何平均值.
- 7 【问题求解】已知
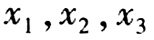的算术平均值为a，
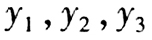的算术平均值为b，则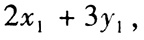
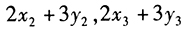的算术平均值为（）。 - A 、2a +3b
- B 、
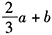
- C 、6a+9b
- D 、2a+b
- E 、以上结论均不正确
- 8 【条件充分性判断】两个数a，b的几何平均值的3倍大于它的算术平均值。（） （1）a，b满足
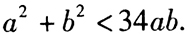（2）a，b均为正数 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 9 【问题求解】已知
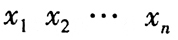的几何平均值为3，前n-1个数的几何平均值为2，则
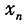的值为（）。 - A 、
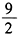
- B 、
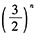
- C 、
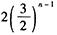
- D 、
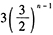
- E 、
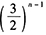
- 10 【问题求解】已知a，b，c是三个正整数，且a>b>c，若a，b，c的算术平均值为
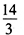，几何平均值为4，且b，c之积恰为a，则a，b，c的值依次为（）。 - A 、6，3，2
- B 、12，6，2
- C 、10，5，2
- D 、8，4，2
- E 、以上结论均不正确
热门试题换一换
- 甲、乙、丙和丁四人进入某围棋邀请赛半决赛，最后要决出一名冠军。张、王和李三人对结果做了如下预测： 张：冠军不是丙。王：冠军是乙。李：冠军是甲。 已知张、王和李三人中一人的预测正确，以下哪项为真（）。
- 李丽和王佳是好朋友，同在一家公司上班，常常在一起喝下午茶，她们发现常去喝下午茶的人或者喜欢红茶，或者喜欢花茶，或者喜欢绿茶。李丽喜欢绿茶，王佳不喜欢花茶。 根据以上陈述，以下哪项必定为真（）。 Ⅰ.王佳如果喜欢红茶，就不喜欢绿茶； Ⅱ.王佳如果不喜欢绿茶，就一定喜欢红茶； Ⅲ.常去喝下午茶的人如果不喜欢红茶，就一定喜欢绿茶或花茶； Ⅳ.常去喝下午茶的人如果不喜欢绿茶，就一定喜欢红茶和花茶。
- 某小区业主委员会的4名成员晨桦、建国、向明和嘉媛围坐在一张方桌前（每边各坐一人）讨论小区大门旁的绿化方案。4人的职业各不相同，每个人的职业是高校教师、软件工程师、园艺师或邮递员中的一种。已知：晨桦是软件工程师，他坐在建国的左手边，向明坐在高校教师的右手边，坐在建国对面的嘉媛不是邮递员。 根据以上信息，可以得出以下哪项（）。
- 年初，为激励员工努力工作，某公司决定根据每月的工作绩效评选“月度之星”。王某在当年前10个月恰好只在连续的4个月中当选“月度之星”，他的另三位同事郑某、吴某、周某也做到了这一点。关于这四人当选“月度之星”的月份，已知： （1）王某和郑某仅有三个月同时当选； （2）郑某和吴某仅有三个月同时当选； （3）王某和周某不曾在同一个月当选； （4）仅有2人在7月同时当选； （5）至少有1人在1月当选。 根据以上信息，王某当选“月度之星”的月份是（）。
- 寻找否定假设的一般思路是：已知论证条件1、2等，又已知论证结论3，问必须假设什么条件才能得出结论3。正确的选项若是A，则A选项需要满足：（1+2+A的否定）→（3的否定）。例如，（ ）+1>2，问，（ ）中的数字必须满足以下哪些假设条件？（多选）
- 某次乒乓球单打比赛中，先将8名选手等分为2组进行小组单循环赛，若一位选手只打了1场比赛后就因故退赛，则小组赛的实际比赛场数是 （）。
- The “threatened” tag disappointed some environmentalists in that it（）.
- Samuel Smiles
亿题库—让考试变得更简单
已有600万用户下载
Vj2GM