- 简答题 设有两门高射炮,每一门击中飞机的概率都是0.6,求: (1)同时各发射一发炮弹而击中飞机的概率是多少? (2)若有一架敌机入侵领空,欲以99%以上的概率击中它,问至少需要配备多少门高射炮?

扫码下载亿题库
精准题库快速提分
 参考答案
参考答案在一个有关概率的应用题中,若题中给出了某事件的概率,则此类题必为独立性的题型。
(1)设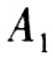 第一门炮击中,
第一门炮击中, 第二门炮击中,则同时各发射一发炮弹而击中飞机的概率是
第二门炮击中,则同时各发射一发炮弹而击中飞机的概率是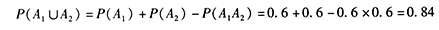 。
。
(2)设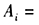 “第i门炮发射一发炮弹而击中敌机”,对第二问,设需配备n门高射炮,依题意
“第i门炮发射一发炮弹而击中敌机”,对第二问,设需配备n门高射炮,依题意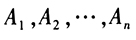 相互独立,
相互独立,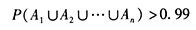 ,则
,则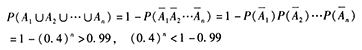 ,解得,
,解得,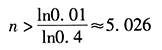 取n=6。故至少需配备6门高射炮,同时各发射一发炮弹,可保证以99%以上的概率击中敌机。
取n=6。故至少需配备6门高射炮,同时各发射一发炮弹,可保证以99%以上的概率击中敌机。
 您可能感兴趣的试题
您可能感兴趣的试题- 1 【条件充分性判断】甲乙两人每次击中目标的概率分别是
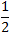 和p。现每人各射击两次,则“甲击中目标的次数减去乙击中目标的次数的差不超过1”的概率为
和p。现每人各射击两次,则“甲击中目标的次数减去乙击中目标的次数的差不超过1”的概率为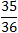 。() (1)
。() (1) (2)
(2)
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和条件(2)单独都不充分,条件(1)和(2)联合起来也不充分
- 2 【简答题】求两人同时击中目标的概率。
- 3 【简答题】求至少有一人击中目标的概率。
- 4 【简答题】求恰好有一人击中目标的概率。
- 5 【问题求解】某射手的命中率为0.7,他连续向一目标射击3次,则至少射中1次的概率为()。
- A 、0.849
- B 、0.857
- C 、0.943
- D 、0.973
- E 、0.985
- 6 【条件充分性判断】某射手在一次射击中,射中的环数低于9环的概率为0.48。() (1)该射手在一次射击中,射中10环的概率为0.24 (2)该射手在一次射击中,射中9环的概率为0.28
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 7 【问题求解】某射手射击一次,击中目标的概率是0.9,他连续射击4次,且各次是否击中相互之间没有影响,则他第2次未击中,其余3次都击中的概率是()。
- A 、0.0729
- B 、0.0792
- C 、0.0139
- D 、0.0579
- E 、0.0569
- 8 【条件充分性判断】甲、乙两人各进行一次射击,至少有1人击中目标的概率为0.84。() (1)在一次射击中,甲击中目标的概率为0.6,乙击中目标的概率为0.5 (2)在一次射击中,甲、乙击中目标的概率都是0.6
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 9 【问题求解】 甲,乙两人各进行3次射击,甲每次击中目标的概率为1/2,乙每次击中目标的概率为2/3,则乙恰好比甲多击中目标两次的概率为()。
- A 、1/6
- B 、1/12
- C 、1/24
- D 、1/36
- E 、1/72
- 10 【问题求解】 某射手每次射击击中目标的概率是2/3,且各次射击的结果互不影响。假设这名射手射击5次,求有3次连续击中目标,另外2次未击中目标的概率p=()。
- A 、
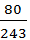
- B 、
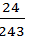
- C 、
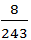
- D 、
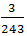
- E 、

热门试题换一换
- Diamonds have little()value and their price depends almost entirely on their scarcity.
- His name was on the()of my tongue, but I just couldn't recall it.
- Advertising are appreciated by manufacturersbecause they().
- 当x=2005,y=1949时,代数式的值为()。
- 实数a,b,c成等比数列。() (1)关于x的一元二次方程有两个相等实数根 (2)lga,lgb,lgc成等差数列
- 《数学通讯》第一期记载:在1742年,德国某中学数学老师哥德巴赫首次提出:任何一个大于6的合数都可以等于两个素数的和。 如果以上《数学通讯》记载的是真实的,以下哪项不可能为真()。 Ⅰ.毕德哥拉斯在公元前1世纪提出:大于6的合数可以表示为两个素数的和。 Ⅱ.中国数学家陈锦润在1970年代证明:大于6的每一个合数都可以等于两个素数的和。 Ⅲ.俄罗斯数学家安德鲁在1880年证明:不是每一个大于6的合数都可以等于两个素数的和。
- The authors of the research article are optimistic because().
- Judging from the context, the word “rub” ( Line 1,Para.3) probably means_____·
- How did Redmon find his job?
亿题库—让考试变得更简单
已有600万用户下载
 o2Ppk
o2Ppk
