环保工程师题库

首页环保工程师题库

单选题多选题

- 1 【单选题】设为三阶实对称矩阵A的特征值，属于的特征向量为的特征向量是:
- A 、
- B 、
- C 、
- D 、
【正确答案：A】

本题考查特征值与特征向量的相关计算性质。
已知重要结论：实对称矩阵属于不同特征值的特征向量必然正交。

查看解析
- 2 【单选题】设A为m ×n矩阵，则齐次线性方程组Ax = 0有非零解的充分必要条件是:
- A 、矩阵A的任意两个列向量线性相关
- B 、矩阵A的任意两个列向量线性无关
- C 、矩阵A的任一列向量是其余列向量的线性组合
- D 、矩阵A必有一个列向量是其余列向量的线性组合
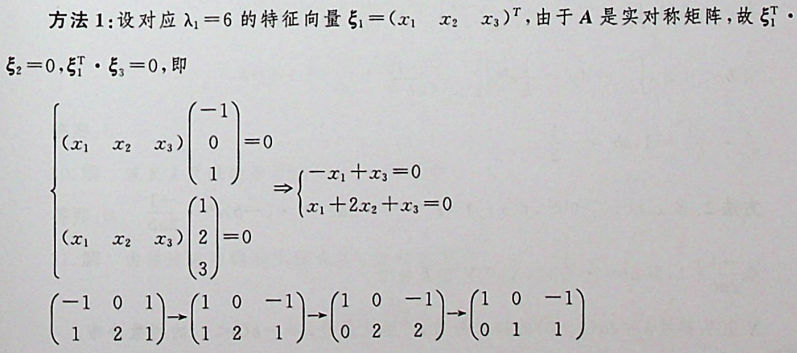
【正确答案：D】

本题考查线性齐次方程组解的基本知识，矩阵的秩和矩阵列向量组的线性相关性。
已知齐次线性方程组Ax=0(其中A为m ×n矩阵），有非零解的充分必要条件是：

设R(A)==r，当r
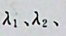
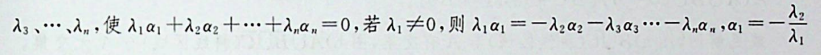
由此可推出矩阵的列向量构成的向量组线性相关，即存在一组不全为零的数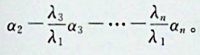矩阵A的列向量整体是线性相关的，但并不能说明A的任意两个列向量也是线性相关的。可举一例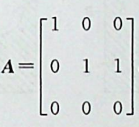这个矩阵对应的齐次方程组就有无穷多解，因为R(A)=2<3,然而矩阵中第一列和第二列或者第三列线性无关，第二列和第三列线性相关，所以选项A、B和C错误。

查看解析
- 3 【单选题】矩阵的逆矩阵是是
- A 、
- B 、
- C 、
- D 、
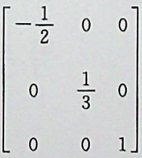
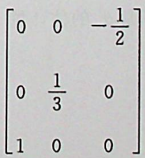
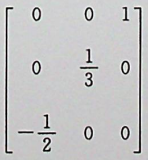
【正确答案：C】

本题考查逆矩阵的求法。方法1:利用初等行变换求解如下：

方法2:逐项代入法，与矩阵A乘积等于E，即为正确答案。验证选项C,计算过程如下：

方法3:利用求方程的逆矩阵方法

查看解析
- 4 【单选题】设，其中φ（u）具有二阶连续导数，则等于：
- A 、
- B 、
- C 、1
- D 、
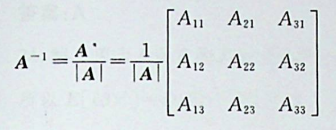
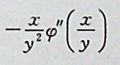
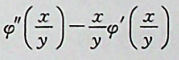
【正确答案：B】

本题考查多元抽象函数偏导数的运算，及多元复合函数偏导数的计算方法。

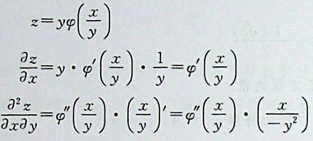
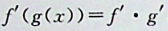注：复合函数的链式法则为，读者应注意题目中同时含有抽象函数与具体函数的求导规则，抽象函数求导就直接加一撤，具体函数求导则利用求导公式。

查看解析
- 5 【单选题】幂级数的和函数s（x）等于:
- A 、
- B 、
- C 、
- D 、cosx
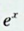
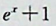
【正确答案：C】

本题考查幂级数的和函数的基本运算。

查看解析
- 6 【单选题】微分方程的特解是：
- A 、
- B 、
- C 、
- D 、
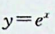
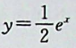
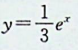
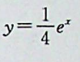
【正确答案：C】

本题考查二阶常系数线性非齐次方程的特解问题。
严格说来本题有点超纲，大纲要求是求解二阶常系数线性齐次微分方程，对于非齐次方程并不做要求。因此本题可采用代入法求解，考虑到观察各选项，易知选项C符合要求。

具体解析过程如下：

查看解析
- 7 【单选题】曲线的拐点是:
- A 、
- B 、
- C 、(一 1，e)
- D 、
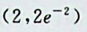
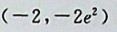
【正确答案：A】

本题考查函数拐点的求法。
求解函数拐点即求函数的二阶导数为0的点，因此有：

查看解析
- 8 【单选题】级数满足下列什么条件时收敛：
- A 、
- B 、
- C 、
- D 、
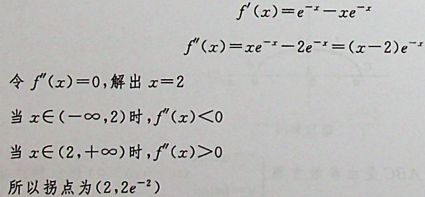
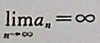
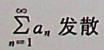
【正确答案：D】

本题考查级数收敛的充分条件。

其他选项均不符合交错级数收敛的判别方法。

查看解析
- 9 【单选题】设L是椭圆 (a>0,b>0)的上半椭圆周，沿顺时针方向，则曲线积分等于:
- A 、
- B 、
- C 、
- D 、
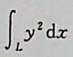
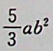
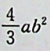
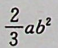
【正确答案：B】

本题考查了参数方程形式的对坐标的曲线积分（也称第二类曲线积分），注意绕行方向为顺时针。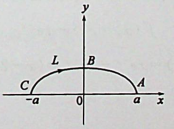
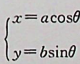如解图所示，上半椭圆ABC是由参数方程(a>0；b>0)画出的。本题积分路径L为沿上半椭圆顺时针方向，从C到B，再到A，θ变化范围由π变化到0, 具体计算可由方程x=aCOSθ沒得到。起点为C(一a，0)，把-a代入方程中的x，得θ=π。终点为A(a,0)，把a代入方程中的x，得 θ=0,因此参数θ的变化为从θ=π变化到θ=0,即θ：丌→0。

由x=acosθ可知，dx = — asinθdθ因此原式有：

注：对坐标的曲线积分应注意积分路线的方向，然后写出积分变量的上下限，本题若取逆时针为绕行方向，则θ的范围应从θ到π。简单作图即可观察和验证。

查看解析
- 10 【单选题】函数在区间[—π，π]上的最小值点等于:
- A 、
- B 、0
- C 、
- D 、π
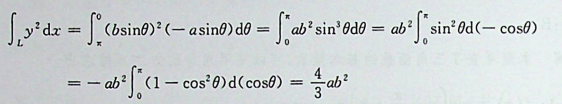
【正确答案：B】

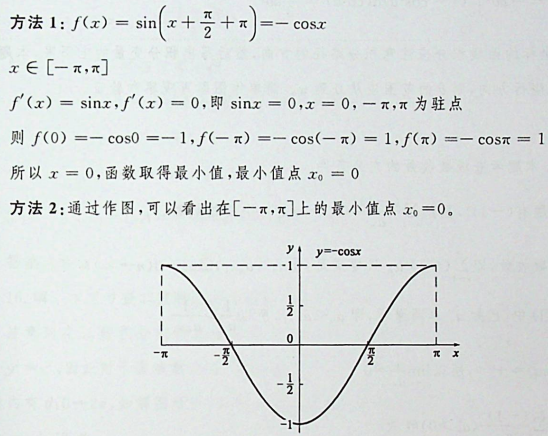
本题考查了三角函数的基本性质，可以采用求导的方法直接求出。

查看解析