- 条件充分性判断数列
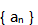 为等比数列,则可以确定等比数列的公比q。() (1)
为等比数列,则可以确定等比数列的公比q。() (1)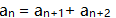 (2)
(2)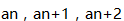 成等差数列
成等差数列 - A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和条件(2)单独都不充分,条件(1)和(2)联合起来也不充分

扫码下载亿题库
精准题库快速提分
 参考答案
参考答案【正确答案:B】
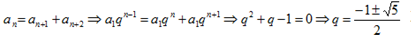 不确定。
不确定。
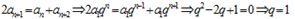 充分。
充分。
 您可能感兴趣的试题
您可能感兴趣的试题- 1 【问题求解】 设等比数列
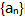 的前n项和为
的前n项和为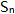 ,且
,且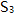 =2,
=2,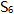 =6,则
=6,则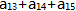 的值是()。
的值是()。 - A 、18
- B 、28
- C 、32
- D 、64
- E 、128
- 2 【条件充分性判断】设
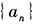 是等比数列,则
是等比数列,则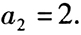 。() (1)
。() (1)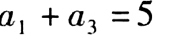 (2)
(2)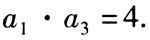
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 3 【条件充分性判断】等比数列
 的前n项和为
的前n项和为 的最小的n值为8。() (1)首项
的最小的n值为8。() (1)首项 (2)公比q=5
(2)公比q=5 - A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 4 【问题求解】
 是公比为q的等比数列
是公比为q的等比数列 的前n项之和,且
的前n项之和,且 是()。
是()。 - A 、公比为nq的等比数列
- B 、公比为
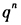 的等比数列
的等比数列 - C 、公比为
 的等比数列
的等比数列 - D 、公比为q的等比数列
- E 、不是等比数列
- 5 【问题求解】等比数列
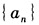 的前n项和为
的前n项和为 成等差数列,则
成等差数列,则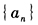 的公比为()。
的公比为()。 - A 、2
- B 、
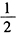
- C 、
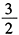
- D 、3
- E 、
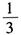
- 6 【问题求解】在等比数列
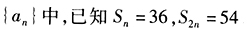 等于 ()。
等于 ()。 - A 、63
- B 、68
- C 、76
- D 、89
- E 、92
- 7 【条件充分性判断】数列
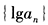 是等差数列。() (1)
是等差数列。() (1)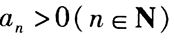 (2)
(2)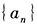 成等比数列
成等比数列 - A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 8 【条件充分性判断】
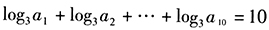 。() (1)在等比数列
。() (1)在等比数列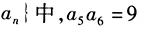 (2)在等比数列
(2)在等比数列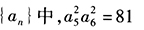
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 9 【条件充分性判断】数列
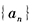 是等比数列。() (1)设
是等比数列。() (1)设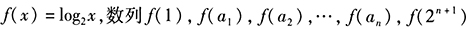 是等差数列 (2)数列
是等差数列 (2)数列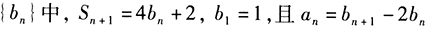
- A 、条件(1)充分,但条件(2)不充分
- B 、条件(2)充分,但条件(1)不充分
- C 、条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
- D 、条件(1)充分,条件(2)也充分
- E 、条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
- 10 【问题求解】 设等比数列
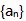 的前n项和为
的前n项和为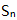 ,且
,且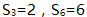 ,则
,则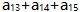 的值是( )。
的值是( )。 - A 、 18
- B 、 28
- C 、 32
- D 、 64
- E 、 128
热门试题换一换
- 参加某国际学术研讨会的60名学者中,亚裔学者31人,博士33人,非亚裔学者中无博士学位的4人。 根据上述陈述,参加此次国际研讨会的亚裔博士有几人?()
- Before Jane_____ (go) to bed, she always_____ (brush) her teeth.
- 任何一个人的身体感染了X病毒,一周以后就会产生抵抗这种病毒的抗体。这些抗体的数量在接下来的大约一年左右的时间内都会增加。现在,有一测试可靠地指出了一个人的身体内存在有多少个抗体。如果确实的话,这个测试可在一个人感染上某种病毒的第一年内被用来估计那个人已经感染上这种病毒多长时间了,估计误差在一个月之内。 下面哪一个结论能被上面的论述最有力地支持()。
- 小张承诺:如果天不下雨,我一定去看足球赛。 以下哪项如果为真,说明小张没有兑现承诺()。 Ⅰ.天没下雨,小张没去看足球赛; Ⅱ.天下雨,小张去看了足球赛; Ⅲ.天下雨,小张没去看足球赛。
- 平行四边形的一个角比它的邻角的2倍还大15°,则相邻两个内角为()。
- 甲、乙、丙三人各自去破译一个密码,他们能译出的概率分别为,则恰有一个人译出的概率为()。
- 设Ω={1,2,3,4,5,6,},A={1,3,5},B={1,4},则()。
- According to the passage, physical exercise can make people_____.
- In the author's view, many endangered languages are_____.
亿题库—让考试变得更简单
已有600万用户下载
 mOP8q
mOP8q
