- 问题求解设点A（0，2）和B（1，0），在线段AB上取一点M（x，y）（0
- A 、
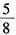
- B 、
- C 、
- D 、
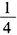
- E 、
扫码下载亿题库
精准题库快速提分
参考答案【正确答案：B】
由点A，B所确定的直线方程为2x+y=2，则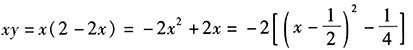
，
当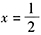
时，xy取最大值
。
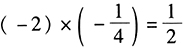您可能感兴趣的试题- 1 【条件充分性判断】直线ax+by+3=0被圆
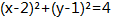截得的线段长度为
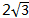。（） （1）a=0，b=-1 （2）a=-1，b=0 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和（2）联合起来也不充分
- 2 【问题求解】 已知A(2，5)，B(4，1)。若点P(x，y)在线段AB上，则2x-y的最大值为（）。
- A 、 -1
- B 、 3
- C 、 7
- D 、 8
- E 、 1
- 3 【问题求解】直线L与圆
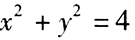相交于A，B两点，且A，B两点中点的坐标为（1，1），则直线乙的方程为（）。 - A 、y-x=1
- B 、y-x=2
- C 、y+x=1
- D 、y+x=2
- E 、2y -3x=1
- 4 【条件充分性判断】直线axbby+3=0被圆
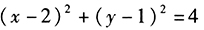截得的线段长度为
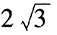。（） （1）a=0，b=-1 （2）a=-1，b=0 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 5 【条件充分性判断】设a，b为实数，则a=1，b=4。（） （1）曲线
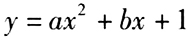与x轴的两个交点的距离为
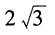（2）曲线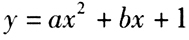
关于直线x+2=0对称 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 6 【条件充分性判断】直线y=ax+b与抛物线
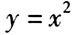有两个交点。（） （1）
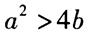（2）b>0 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 7 【问题求解】已知两点
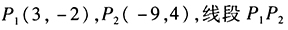与x轴的交点P分有向线段
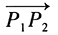所成比为λ，则有（）。 - A 、λ=2，P（1，0）
- B 、λ=-2，P（-1，0）
- C 、λ=
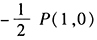
- D 、
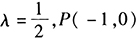
- E 、以上结论均不正确
- 8 【问题求解】已知3个点，A（x,5）,B（-2,y）,C（1,1）,若点C是线段AB的中点，则（）。
- A 、x=4,y=-3
- B 、x=0,y=3
- C 、x=0,y=-3
- D 、x=-4,y=-3
- E 、x-3,y=-4
- 9 【问题求解】已知定点A（2，-3），B（-3，-2），直线l过点P（1，1）且与线段AB相交于点M，则直线l的斜率k的取值范围为（）。
- A 、
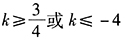
- B 、
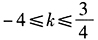
- C 、
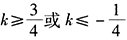
- D 、
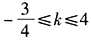
- E 、
- 10 【条件充分性判断】 直线y=ax+b与抛物线y=x2有两个交点。（） （1）
（2）b＞0 - A 、条件（1）充分，条件（2）不充分
- B 、条件（2）充分，条件（1）不充分
- C 、条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
热门试题换一换
- Franklin D.Roosevelt argued that the depression stemmed from the American economy's（）flaws.
- Various efforts have been made over the centuries to predict earthquakes, including observing lightsin the sky and（）animal behavior.
- 近年来，越来越多的教育专家不断呼吁小学生家长不要给孩子增加太多的学习负担，少报课外班，过多地上课外班对小学生的心理健康不利。现在社会上充斥着各类针对小学生的课外培训机构，良莠不齐。 以下哪项陈述为真，最有力地支持了教育专家的观点（）。
- 李娜说，作为一个科学家，她知道没有一个科学家喜欢朦胧诗，而绝大多数科学家都擅长逻辑思维。因此，至少有些喜欢朦胧诗的人不擅长逻辑思维。 以下哪项的推理结构和题干的推理结构最为类似（）。
- 某本科专业按如下原则选拔特别奖学金的候选人：将本专业的同学按德育情况排列名次，均分为上、中、下三个等级（即三个等级的人数相等，下同），候选人在德育方面的表现必须为上等；将本专业的同学按学习成绩排列名次，均分为优、良、中、差四个等级，候选人的学习成绩必须为优；将本专业的同学按身体状况排列名次，均分为好与差两个等级，候选人的身体状况必须为好。 假设该专业共有36名本科学生，则除了以下哪项外，其余都可能是这次选拔的结果（）。
- 孔智、孟睿、荀慧、庄聪、墨灵、韩敏等6人组成一个代表队参加某次棋类大赛。其中两人参加围棋比赛，两人参加中国象棋比赛，还有两人参加国际象棋比赛。有关他们具体参加比赛项目的情况还需满足以下条件： （1）每位选手只能参加一个比赛项目； （2）孔智参加围棋比赛，当且仅当，庄聪和孟睿都参加中国象棋比赛； （3）如果韩敏不参加国际象棋比赛，那么墨灵参加中国象棋比赛； （4）如果荀慧参加中国象棋比赛，那么庄聪不参加中国象棋比赛； （5）荀慧和墨灵至少有一人不参加中国象棋比赛。 如果庄聪和孔智参加相同的比赛项目，且孟睿参加中国象棋比赛，那么可以得出以下哪项（）。
- 陈先生：未经许可侵入别人的计算机，就好像开偷来的汽车撞伤了人，这些都是犯罪行为。但后者性质更严重，因为它既侵占了有形财产，又造成了人身伤害；而前者只是在虚拟世界中捣乱。 林女士：我不同意。例如，非法侵入医院的计算机，有可能扰乱医疗数据，甚至危及病人的生命。因此，非法侵入计算机同样会造成人身伤害。 以下哪项最为准确地概括了两人争论的焦点（）。
- 若x和y是整数，则xy+1能被3整除。（） （1）当x被3除时，其余数为1 （2）当y被9除时，其余数为8
- 为了了解高中毕业生的身体状况，某校特意选取两组高中毕业生进行体能测试。经测试发现：第一组学生的体能合格率达到了60%，而第二组的体能合格率只有20%。学校据此得出结论：该校高中毕业生的身体状况存在很大的差异。 以下哪项最能削弱以上结论（）。
- According to Paragraph 5,George Osborne may（）.
亿题库—让考试变得更简单
已有600万用户下载
ddnoL