- 简答题
题干：袋中装有5只白球，6只黑球，依次取4只。
题目：每次取1只（取后放回），则第二次取到白球的取法共有多少种？
扫码下载亿题库
精准题库快速提分
参考答案这是一种典型的排队问题，设有四个位置（如图所示）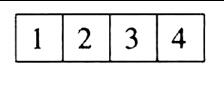
分四个步骤完成，先取一个白球放到第2号位置，共有5种取法，再分别依次取球放入1，3，4号位置，每个步骤都有11种取法，从而由乘法原理，总取法为5×11×11×11=6655（种）。
您可能感兴趣的试题- 1 【问题求解】 设f（x）是二次多项式，且f（2）= f（-1）=0，f（1）=-4，则f（0）=（）。
- A 、-10
- B 、-8
- C 、6
- D 、0
- E 、-4
- 2 【条件充分性判断】设a是整数，则a=2。（） （1）一元二次方程
有实根 （2）一元二次方程
有实根 - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 3 【简答题】“只有1个次品”的抽法有多少种？
- 4 【简答题】至多有1只黑球的不同取法共有多少种？
- 5 【简答题】每次取1只（取后不放回），则共有多少种不同取法？
- 6 【简答题】每次取1只（取后放回），则共有多少种不同取法？
- 7 【简答题】每次取1只（取后不放回），则第二次取到白球的取法共有多少种？
- 8 【问题求解】一元二次函数x（1-x）的最大值为（）。
- A 、0.05
- B 、0.10
- C 、0.15
- D 、0.20
- E 、0.25
- 9 【条件充分性判断】一次函数y=(m+1)x+m-1的图像不经过第一象限。（） （1）一元二次方程-2x+m=0有实数根 （2）一元二次方程-mx+2 =0有实数根
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 10 【条件充分性判断】一次函数y=（m+1）x+m-1的图像不经过第一象限。（） （1）一元二次方程
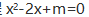（2）一元二次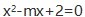
- A 、条件（1）充分，但条件（2）不充分
- B 、 条件（2）充分，但条件（1）不充分
- C 、 条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和（2）联合起来也不充分
热门试题换一换
- 鸽子走路时，头部并不是有规律地前后移动，而是一直在往前伸。行走时，鸽子脖子往前一探，然后，头部保持静止，等待着身体和爪子跟进。有学者曾就鸽子走路时伸脖子的现象做出假设：在等待身体跟进的时候，暂时停止的头部有利于鸽子获得稳定的视野，看清周围的事物。 以下哪项如果为真，最能支持上述假设（）。
- Itis very hard to establish a law against appearance discrimination in that（）.
- 整个队列的人数是35。（） （1）甲、乙两人排队买票，甲后面有10人，而乙前面有20人 （2）甲、乙两人排队买票，甲、乙之间有3人
- （8）
- The theoretical separation of living，working，traffic and recreation has led to_____.
- According to Paragraph 3，the newest group of singles are_____.
- According to the author, one of the driving forces behind M&A wave is_____.
- The author begins his article with Edmund Burke's words to_____.
亿题库—让考试变得更简单
已有600万用户下载
RP8AW