一平面简谐波的波动方程为则在t=0.25s时处于平衡位置，且与坐标原点x=0最近的质元的位置是( )_结构工程师题库

单选题一平面简谐波的波动方程为则在t=0.25s时处于平衡位置，且与坐标原点x=0最近的质元的位置是( )。
A 、 x=±5m
B 、 x=5m
C 、 x=±1.25m
D 、x=1.25m

扫码下载亿题库

精准题库快速提分

参考答案

【正确答案：C】

在t=0.25s时刻，处于平衡位置，y=0，由简谐波的波动方程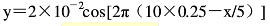=0可知，cos[2π (10X0.25-x/5) ]=0，则2π (10X0.25-x/5) = (2k+1) π/2 (k=0， ±1，±2，…)。由此可得：x=5 (9/4－1k/2)。当x=0时，k=9/2。所以k取，或5；x=±1.25 时，与坐标原点x=0最近。

您可能感兴趣的试题

- 1 【单选题】一平面简谐波的波动方程为对x=-2.5m处的质元，在t=0.25s时，它的( )。
- A 、动能最大，势能最大
- B 、动能最大，势能最小
- C 、动能最小，势能最大
- D 、动能最小，势能最小
答案解析
- 2 【单选题】一平面简谐波的波动方程为y=0.01cos10π（25t-x）（SI），则在t=0.1s时刻， x=2m处质元的振动位移是（）。
- A 、0.01cm
- B 、0.01m
- C 、-0.01m
- D 、0.01mm
答案解析
- 3 【单选题】一平面简谐波的波动方程为y=2×cos2π[10t- (x/5) ] (SI)，t=0.25s时处于平衡位置、且与坐标原点x=0最近的质元的位置是（）。
- A 、x=±5m
- B 、x=5m
- C 、x=±1.25m
- D 、x=1.25m
答案解析
- 4 【单选题】一平面简谐波的波动方程为对x=－2.5m处的质元，在t=0.25s时，它的( )
- A 、动能最大，势能最大
- B 、动能最大，势能最小
- C 、动能最小，势能最大
- D 、动能最小，势能最小
答案解析
- 5 【单选题】一平面简谐波的波动方程为y=0.02cosπ (50t+4x) (SI)，此波的振幅和周期分别为( )。
- A 、0.02cm，0.04s
- B 、0.02m，0.02s
- C 、－0.02m，0.02s
- D 、0.02m，25s
答案解析
- 6 【单选题】一平面简谐波的波动方程为y=0.01cos10π (25t-x) (SI)，则在t=0.1s时刻，x= 2m处质元的振动位移是( )。
- A 、0.01cm
- B 、0.01m
- C 、－0.01m
- D 、0.01mm
答案解析
- 7 【单选题】已知平面简谐波的方程为y=Acos（Bt-C×），式中A、B、C为正常数，此波的波长和波速分别为（）。
- A 、B/C，2π/C
- B 、2π/C，B/C
- C 、π/C，2B/C
- D 、2π/C，C/B
答案解析
- 8 【单选题】一平面简谐波的波动方程为y=0.01cos10π（25t-x）（SI），则在t=0.1s时刻，x=2m处质元的振动位移是（）。
- A 、0.01m
- B 、0.01m
- C 、-0.01m
- D 、0.01mm
答案解析
- 9 【单选题】一平面简谐波的波动方程为y=0.02cosπ（50t+4x）（SI），此波的振幅和周期分别为（）。
- A 、0.02m，0.04s
- B 、0.02m，0.02s
- C 、-0.02m，0.02s
- D 、0.02m，25s
答案解析
- 10 【单选题】已知平面简谐波的方程为y=Acos（Bt-Cx），式中A、B、C为正常数，此波的波长和波速分别为（）。
- A 、B/C，2π/C
- B 、2π/C，B/C
- C 、π/C，2B/C
- D 、2π/C，C/B
答案解析

找回密码

绑定手机号

重置密码成功

注册成功