- 问题求解若数列
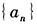的前n项和
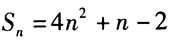，则它的通项公式是（）。 - A 、
- B 、
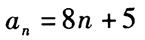
- C 、
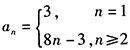
- D 、
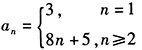
- E 、以上结论均不正确
扫码下载亿题库
精准题库快速提分
参考答案【正确答案：C】
由已知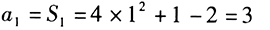
当n≥2时，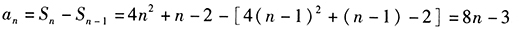
将n=1代入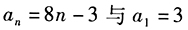
不符，从而其通项为
。
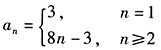您可能感兴趣的试题- 1 【条件充分性判断】 已知数列
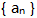为等差数列，公差为d，
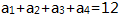，则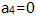
。（） （1）d=-2 （2）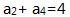
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 2 【条件充分性判断】 已知
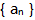为等差数列，则该数列的公差为零。（） （1）对任何正整数n，都有
（2）
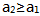
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和条件（2）单独都不充分，条件（1）和（2）联合起来也不充分
- 3 【条件充分性判断】 已知数列
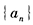为等差数列，公差为d，
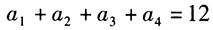，则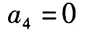
。（） （1）d=-2 （2）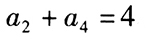
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 4 【条件充分性判断】已知
为等差数列，则该数列的公差为零。（） （1）对任何正整数n，都有
（2）
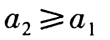
- A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 5 【简答题】已知数列
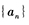的前n项和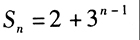
，求通项公式，并判断29和162是否是该数列中的项。
- 6 【问题求解】已知数列
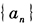的前n项和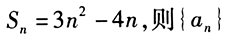
的通项公式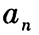
=（）。 - A 、3n-4
- B 、4n-5
- C 、5n-6
- D 、6n-7
- E 、以上结论均不正确
- 7 【条件充分性判断】数列a，b，c是等差数列，不是等比数列。（） （1）a，b，c满足关系式
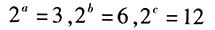（2）a=b=c - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 8 【条件充分性判断】a=330。（） （1）
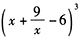的展开式中，x项的系数为a （2）
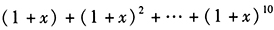的展开式中，
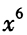项的系数为a - A 、条件（1）充分，但条件（2）不充分
- B 、条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、条件（1）充分，条件（2）也充分
- E 、条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
- 9 【问题求解】 若x取整数，则使分式
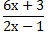的值为整数的x值有（）。 - A 、 2
- B 、 3
- C 、4
- D 、 6
- E 、 8
- 10 【条件充分性判断】 数列
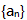是等比数列。（） （1）数列
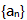的前n项和
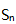满足关系式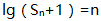
（2）数列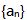
的前n项和
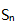满足关系式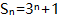
- A 、 条件（1）充分，但条件（2）不充分
- B 、 条件（2）充分，但条件（1）不充分
- C 、条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分
- D 、 条件（1）充分，条件（2）也充分
- E 、 条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
热门试题换一换
- 方程 的两根之差与 的两根之差相等。（） （1）p=q （2）p+q=-4
- The political future of the president is now hanging by a( ).
- When the whole area was（）by the flood, the government sent food there by helicopter.
- 陈先生：未经许可侵入别人的计算机，就好像开偷来的汽车撞伤了人，这些都是犯罪行为。但后者性质更严重，因为它既侵占了有形财产，又造成了人身伤害；而前者只是在虚拟世界中捣乱。 林女士：我不同意。例如，非法侵入医院的计算机，有可能扰乱医疗数据，甚至危及病人的生命。因此，非法侵入计算机同样会造成人身伤害。 以下哪项最为准确地概括了两人争论的焦点（）。
- 将多项式因式分解为（2x-1）q（x），则q（x）等于（）。
- 某班级有18名男生，12名女生，从中选举3名班干部，则所选出的干部为2男1女以及至少2名女生的概率分别为（）。
- 直线和圆C：有交点。（） （1）点在圆C的外部 （2）点不在圆C的内部
- （13）
- （20）
亿题库—让考试变得更简单
已有600万用户下载
3gvG3