
Point and Interval Estimates of the Population Mean

Distribution of the Sample Mean

National Economic Accounts and the Balance of Payments
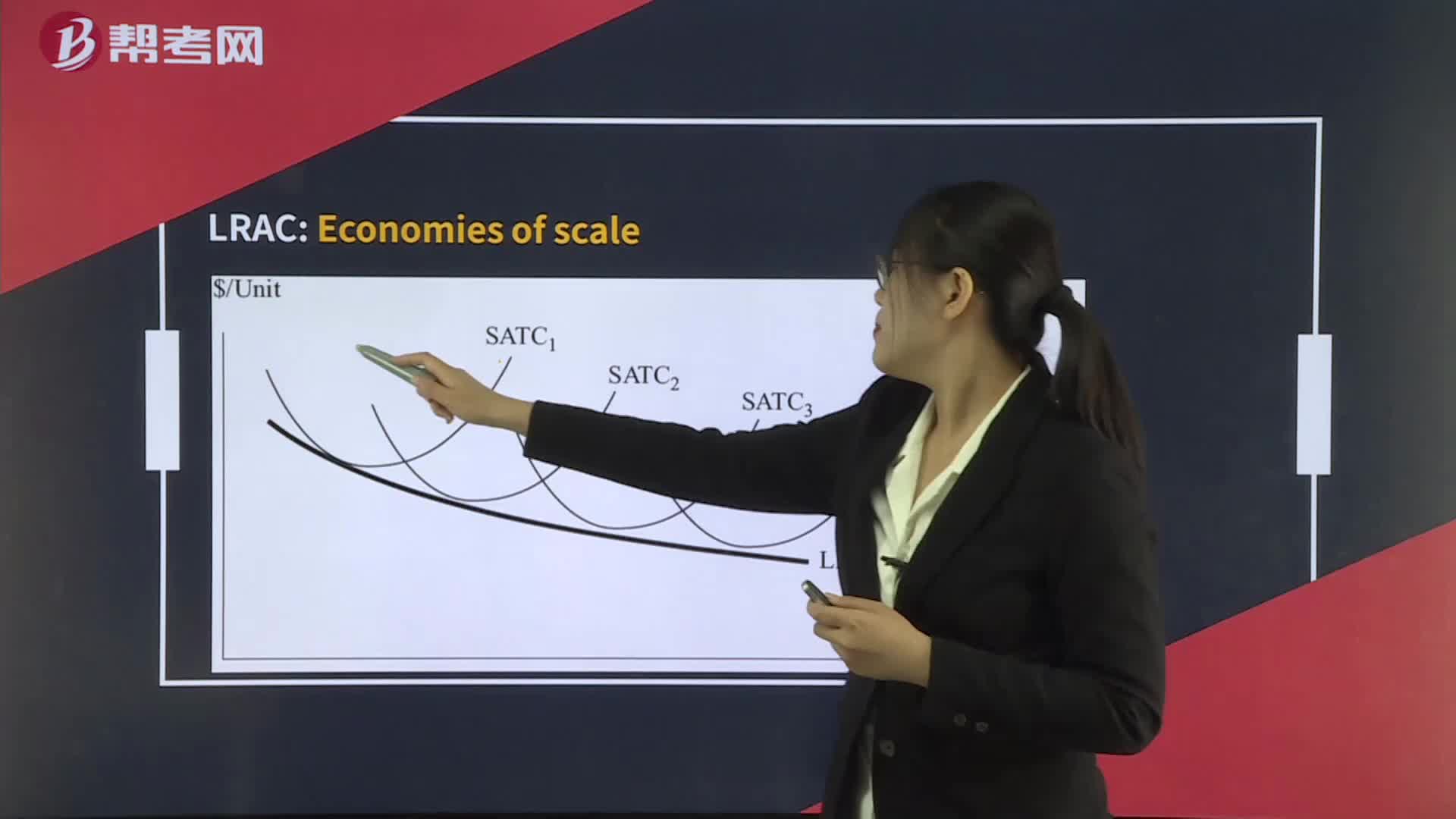
Economies of Scale and Diseconomies of Scale

Hypothesis Tests Concerning the Mean

The Roles of Central Banks

The Quantity Theory of Money

The Roles of Central Banks

The Objectives of Monetary Policy

The Functions of Money

The Costs of Inflation

The Construction of Price Indexes

下载亿题库APP
联系电话:400-660-1360













