
下载亿题库APP
联系电话:400-660-1360

下载亿题库APP
联系电话:400-660-1360

请谨慎保管和记忆你的密码,以免泄露和丢失

请谨慎保管和记忆你的密码,以免泄露和丢失
什么是多元线性回归模型分析?
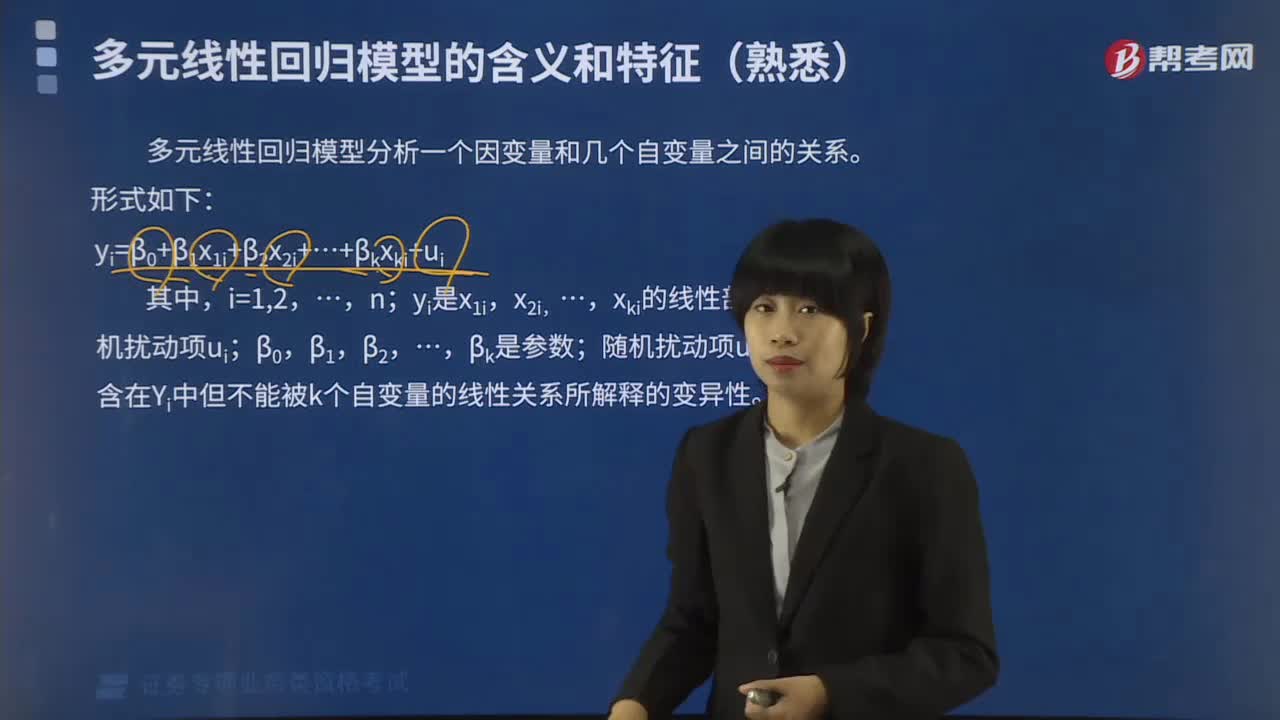
多元线性回归模型分析一个因变量和几个自变量之间的关系。形式如下:
yi=β0+β1x1i+β2x2i+…+βkxki+ui
其中,i=1,2,…,n;yi是x1i,x2i,…,xki的线性部分加上随机扰动项ui;β0,β1,β2,…,βk是参数;随机扰动项ui指的是包含在Yi中但不能被k个自变量的线性关系所解释的变异性。
多元线性回归模型满足如下基本假定:
一、零均值假定,即:
E(ui)=0(i=1,2,…,n)。
二、同方差与无自相关假定,即随机扰动项的方差和协方差满足:
Var(ui)=σ2=常数(i=1,2,…,n),
Cov(ui,uj)=0(i≠j)
三、无多重共线性假定,即解释变量之间不存在线性关系。
四、随机扰动项与解释变量互不相关,即:
Cov(ui,xji)=0(i=1,2,…,n;j=1,2,…,k)。
五、正态性假定,随机扰动项ui 服从正态分布,
即ui~N(0,σ2)。
在多元线性归回中可以使用:最小二乘法,可决系数。修正可决系数:
其中,n为样本容量,k为解释变量的个数,修正的可决系数与R2不同的是:随着解释变量的增多,的值可能变小,甚至可能为负值。
下面给大家提供一道证券投资分析师考试的例题,希望大家认真理解,尽快掌握这个知识点。
【例题】建立黄金价格与美元指数回归模型分析
以2015年2月2月至2015年3月16日美元指数为解释变量x,同期的黄金现货价格(y,美元/盎司)为被解释变量,样本容量为31,建立一元线性回归模型。
【答案】
1. 第一步:散点图直观分析与相关系数计算
2. 通过散点图发现,x与y呈明显负相关关系,求相关系数。结果为-0.843,表明线性关系程度高。
3. 参数估计
a. 预测变量:(常量),x。
a. 因变量:y。
b. 预测变量:(常量),x。
 230
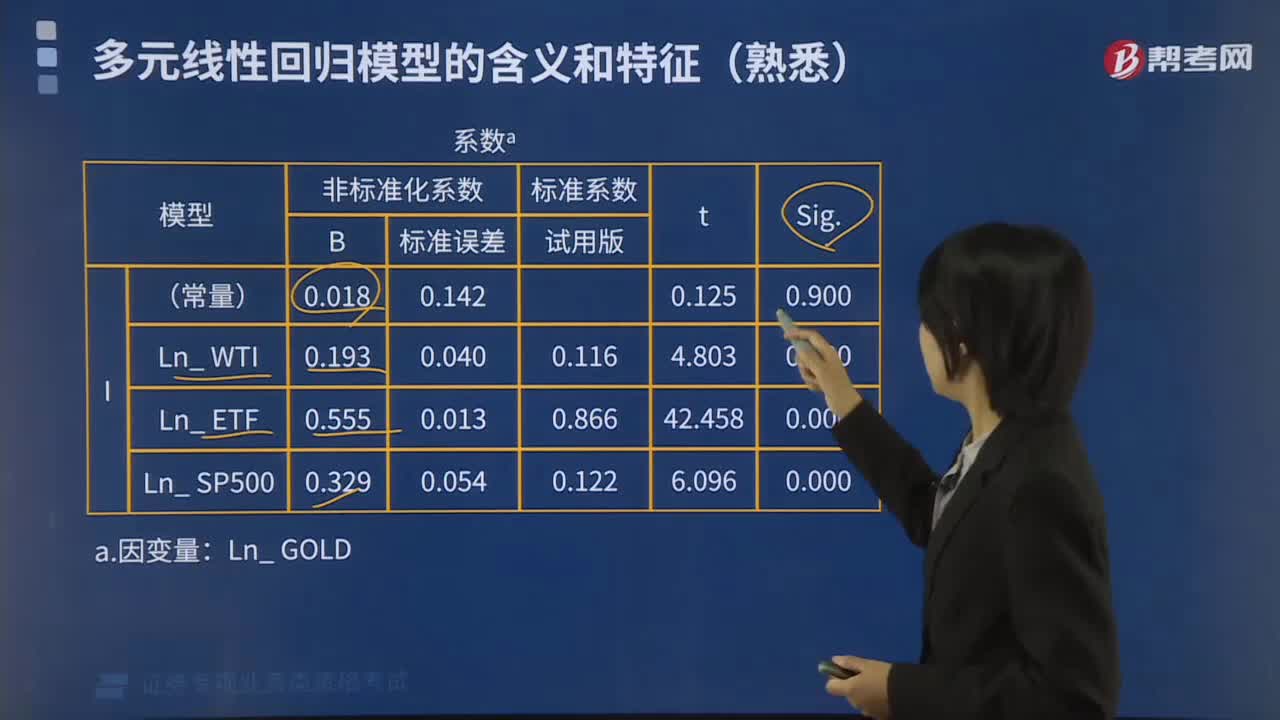
230多元线性回归模型检验的方法有哪些?:多元线性回归模型的检验方法有:判定系数检验(R检验),回归系数显著性检验(T检验),回归方程显著性检验(F检验)。说明模型对样本的拟合效果较好:说明回归方程线性关系显著。即纽约原油价格(WTI)、黄金ETF持仓(吨)和美国标准普尔500指数联合起来对对黄金价格产生显著影响:3个变量的t值对应的sig.均为0.0000.05,说明各回归系数均通过显著性检验。
 329
329多元线性回归模型如何进行应用?:多元线性回归模型如何进行应用?多元线性回归模型的应用:二回归模型的预测。可以预测2015年3月17日黄金现货价格约为1149.982(1150.00936)美元盎司。平均值的预测区间约为(1134.252,个别值的预测区间约为(1108.564,【例题】建立分析影响黄金价格的多元线性回归模型。为分析纽约原油价格(WTI)、黄金ETF持仓(吨)和美国标准普尔500指数对黄金价格的影响。
 833
833什么是多元线性回归模型分析?:多元线性回归模型分析一个因变量和几个自变量之间的关系。xki的线性部分加上随机扰动项ui,随机扰动项ui指的是包含在Yi中但不能被k个自变量的线性关系所解释的变异性:多元线性回归模型满足如下基本假定,E(ui)=0(i=1,即随机扰动项的方差和协方差满足,Var(ui)=σ2=常数(i=1,uj)=0(i≠j)。三、无多重共线性假定,即解释变量之间不存在线性关系:
 01:31
01:312020-05-15
 04:30
04:302020-05-15
 00:49
00:492020-05-15
 00:38
00:382020-05-15
 04:09
04:092020-05-15

微信扫码关注公众号
获取更多考试热门资料