
下载亿题库APP
联系电话:400-660-1360

下载亿题库APP
联系电话:400-660-1360

请谨慎保管和记忆你的密码,以免泄露和丢失

请谨慎保管和记忆你的密码,以免泄露和丢失

2019年MBA考试《数学》考试共25题,分为问题求解和条件充分性判断。小编为您整理第四章 方程与不等式5道练习题,附答案解析,供您备考练习。
1、实数k的取值范围是(-∞,2)∪(5,+∞)。()
(1)关于x的方程kx+2=5x+k的根是非负实数
(2)抛物线 位于x轴上方【条件充分性判断】
位于x轴上方【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:E
答案解析:由条件(1),(k-5)x=k-2,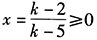 解得 k>5或k≤2,因此条件(1)不充分。
解得 k>5或k≤2,因此条件(1)不充分。
由条件(2),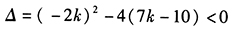 成立,整理得
成立,整理得 ,条件(2)也不充分。
,条件(2)也不充分。
2、自然数n满足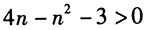 ()
()
(1)自然数n加上2后是一个完全平方数
(2)自然数n减去1后是一个完全平方数【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:C
答案解析:不等式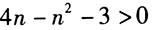 的解集为1<n<3,若n为自然数,则必须n=2。
的解集为1<n<3,若n为自然数,则必须n=2。
由条件(1),令n=23,则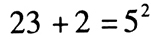 ,但n≠2。
,但n≠2。
由条件(2),令n=17,则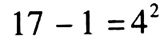 ,但n≠2。因此,条件(1)和条件(2)单独都不充分。
,但n≠2。因此,条件(1)和条件(2)单独都不充分。
联合条件(1)和条件(2),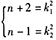 ,这里
,这里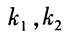 都是正整数,且显然有
都是正整数,且显然有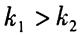 ,从而
,从而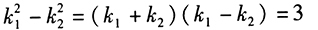
则 ,得
,得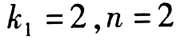 。
。
3、函数 的定义域是()。【问题求解】
的定义域是()。【问题求解】
A.(-∞,4]∪[5,+∞)
B.(-∞,4)
C.
D.
E.
正确答案:C
答案解析:f(x)的定义域为不等式组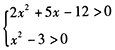 的解集,可得
的解集,可得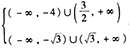 ,因此,f(x)的定义域是
,因此,f(x)的定义域是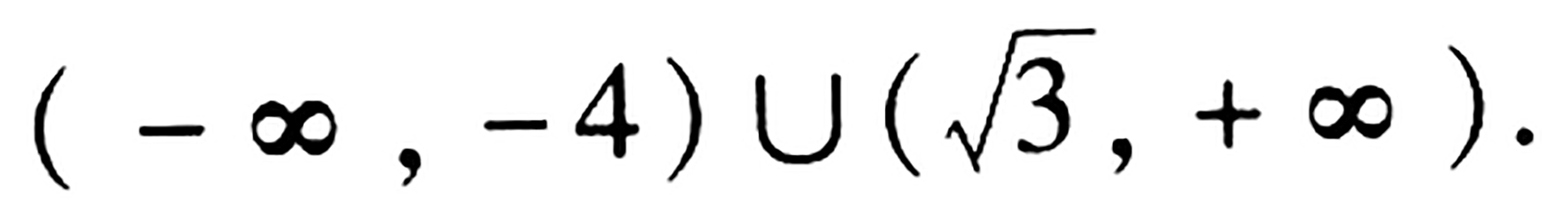
4、已知x,y,z为不相等的实数, ()。【问题求解】
()。【问题求解】
A.1
B.2
C.
D.
E.
正确答案:A
答案解析:此题可直接用代入法,由已知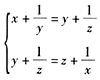 ,令y=1,得
,令y=1,得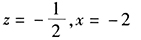 x= -2,因此
x= -2,因此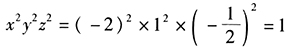 。
。
5、 ()
()
(1)f(x)=(x+1)(x+2)(x+3)-7 ×8 ×9
(2)f(x)=(x+1)(x+2)(x+3)-6 ×7 ×8【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:B
答案解析:取x=-1,x= -2,x= -3,x=5,由条件(1),f(5)≠O,f(-1)=f(-2)=f(-3)=-7×8×9;
由条件(2),f(5)=0,f(-1)=f(-2)=f(-3)=-6×7×8;
而题干中f(5)=0,f(-1)=-6×56,f(-2)=-7×48,f(-3)=-8×42,从而知条件(1)不充分,条件(2)充分。
 05:31
05:312020-05-15
 02:38
02:382020-05-15
 04:04
04:042020-05-15
 03:35
03:352020-05-15
 04:00
04:002020-05-15

微信扫码关注公众号
获取更多考试热门资料