
下载亿题库APP
联系电话:400-660-1360

下载亿题库APP
联系电话:400-660-1360

请谨慎保管和记忆你的密码,以免泄露和丢失

请谨慎保管和记忆你的密码,以免泄露和丢失

2019年MBA考试《数学》考试共25题,分为问题求解和条件充分性判断。小编为您整理精选模拟习题10道,附答案解析,供您考前自测提升!
1、n为任意正整数,则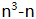 必有约数(因数)()。【问题求解】
必有约数(因数)()。【问题求解】
A.4
B.5
C.6
D.7
E.8
正确答案:C
答案解析: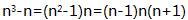 ,在三个连续的整数中必有一个是3的倍数,在两个连续的整数中必有一个是2的倍数(即偶数),因此3|(
,在三个连续的整数中必有一个是3的倍数,在两个连续的整数中必有一个是2的倍数(即偶数),因此3|(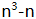 ),2|(
),2|(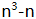 ),从而[3,2] =6可整除
),从而[3,2] =6可整除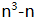 ,即6是
,即6是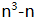 的约数。
的约数。
注:此题可直接取n=2代入得到答案。
2、x-2是多项式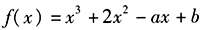 的因式。()
的因式。()
(1)a=1,b=2
(2)a=2,b=3【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:E
答案解析:若x-2是f(x)的因式,即f(x)=(x-2)q(x),
因此, ,即必有16-2a+b=0,
,即必有16-2a+b=0,
因此,条件(1)和条件(2)单独和联合起来都不充分.
3、多项式f(x)除以x+1所得余式为2。()
(1)多项式f(x)除以 所得的余式是x+5
所得的余式是x+5
(2)多项式f(x)除以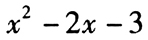 所得的余式是x+3【条件充分性判断】
所得的余式是x+3【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:B
答案解析:题干要求f(x)=q(x)(x+1)+2,即f(-1)=2。
由条件(1),f(x)=q(x)(x-2)(x+1)+(x+5),得f(-1)=4,因此条件(1)不充分;
由条件(2),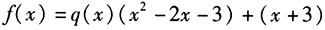 ,得f(-1)=2,因此条件(2)是充分的。
,得f(-1)=2,因此条件(2)是充分的。
4、已知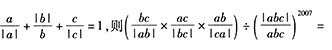 ()。【问题求解】
()。【问题求解】
A.1
B.-1
C.2
D.-2
E.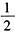
正确答案:B
答案解析:由已知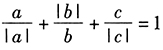 ,a,b,c只能是两正一负,不妨设a>0,b>0,c<0,则
,a,b,c只能是两正一负,不妨设a>0,b>0,c<0,则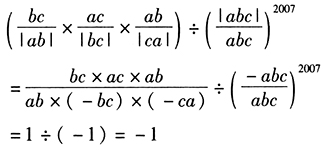
5、长方体的三条棱长成等差数列,最短的棱长为a,三条棱长的和为6a,那么它的全面积是()。【问题求解】
A.
B.
C.
D.
E.
正确答案:D
答案解析:设三条棱长分别为a,a+d,a+2d,由已知a+a+d+a+2d=6a,则有d=a,因此全面积
6、在伯努利试验中,事件A出现的概率为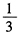 ,则在此3重伯努利试验中,事件A出现奇数次的概率是()。【问题求解】
,则在此3重伯努利试验中,事件A出现奇数次的概率是()。【问题求解】
A.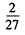
B.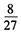
C.
D.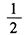
E.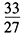
正确答案:C
答案解析:由已知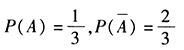 n=3,则所求事件的概率为
n=3,则所求事件的概率为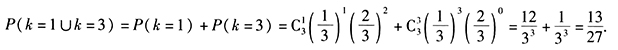
7、已知a+b+c=0,abc =8,则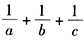 的值()。【问题求解】
的值()。【问题求解】
A.大于零
B.等于零
C.大于等于零
D.小于零
E.小于等于零
正确答案:D
答案解析:
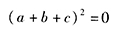 ,即
,即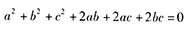 ,因而
,因而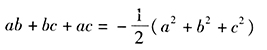 。
。
因为abc =8,即a,b,c都不等于零,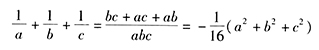 ,从而
,从而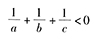 。
。
8、(2008年)点 (2,3)关于直线x+y=0的对称点是()。【问题求解】
(2,3)关于直线x+y=0的对称点是()。【问题求解】
A.(4,3)
B.(-2,-3)
C.(-3,-2)
D.(-2,3)
E.(-4,-3)
正确答案:C
答案解析:设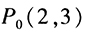 关于直线x+y =0的对称点是
关于直线x+y =0的对称点是 ,则
,则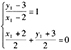 。解得
。解得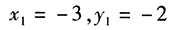 。
。
9、Ⅳ=864。()
(1)从1~8这8个自然数中,任取2个奇数、2个偶数,可组成Ⅳ个不同的四位数
(2)从1~8这8个自然数中,任取2个奇数,作为千位和百位数字,取2个偶数,作为十位和个位数字,可组成Ⅳ个不同的四位数【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:A
答案解析:
由条件(1),在1~8中共有4个奇数、4个偶数,任取2个奇数、2个偶数可组成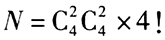 个不同的四位数,即 N=6×6×24=864(个),即条件(1)充分。
个不同的四位数,即 N=6×6×24=864(个),即条件(1)充分。
由条件(2)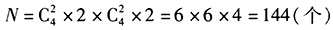 ,即条件(2)不充分。
,即条件(2)不充分。
10、一头病牛服用某种药品后被治愈的可能性为95%,则服用这种药的4头病牛至少有3头被治愈的概率约为()。【问题求解】
A.0.97
B.0.98
C.0.99
D.0.991
E.以上结论均不正确
正确答案:C
答案解析:这是一个4重的伯努利试验。设A:4头病牛至少有3头被治愈,则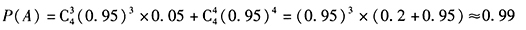
 05:31
05:312020-05-15
 02:38
02:382020-05-15
 04:04
04:042020-05-15
 03:35
03:352020-05-15
 04:00
04:002020-05-15

微信扫码关注公众号
获取更多考试热门资料