这几道数学题怎么做?财富值不够我可以再给你加。但是请把这几道题的详细解答说一下 

这几道数学题怎么做?财富值不够我可以再给你加。但是请把这几道题的详细解答说一下 ![]()

最佳答案
新兵答主 04-02 TA获得超过6350个赞 2023-04-02 10:02
非常感谢您的信任和支持。以下是这几道数学题的详细解答:
1. 求解方程:$\sqrt{2x-1}+\sqrt{6-2x}=2$
首先,由于根号内的式子必须非负,所以要求 $2x-1\geq 0$ 和 $6-2x\geq 0$,解得 $x\in[\frac{1}{2},3]$。
接下来,我们可以利用平方的方法来消去根号。将方程两边平方,得到:
$$2x-1+2\sqrt{(2x-1)(6-2x)}+6-2x=4$$
化简一下,得到:
$$\sqrt{(2x-1)(6-2x)}=1$$
再次平方,得到:
$$(2x-1)(6-2x)=1$$
展开化简,得到二次方程:
$$4x^2-16x+13=0$$
利用求根公式,解得:
$$x=2+\frac{\sqrt{3}}{2},2-\frac{\sqrt{3}}{2}$$
但是,我们需要验证这两个解是否满足原方程的定义域。经过计算,我们发现 $2+\frac{\sqrt{3}}{2}otin[\frac{1}{2},3]$,因此舍去,最终的解为 $x=2-\frac{\sqrt{3}}{2}$。
2. 已知 $a,b,c$ 均为正整数,且满足 $a^2+b^2=c^2$,求所有满足 $a+b+c=1000$ 的三元组 $(a,b,c)$。
根据勾股定理,我们可以列出以下条件:
$$\begin{cases}a^2+b^2=c^2\\a+b+c=1000\end{cases}$$
将第二个式子变形,得到:
$$c=1000-a-b$$
代入第一个式子,得到:
$$a^2+b^2=(1000-a-b)^2$$
展开化简,得到:
$$a^2+b^2=10^6-2000a-2000b+2ab$$
移项整理,得到:
$$(a+b-500)^2=250000-c^2$$
因为 $a,b,c$ 均为正整数,所以 $c$ 的取值范围为 $1\leq c<500$。因此,我们只需要枚举 $c$,计算出所有满足条件的 $a,b$ 即可。
具体来说,我们可以枚举 $c$,然后在 $1\leq a+b<1000-c$ 的范围内,计算出所有满足 $(a+b-500)^2=250000-c^2$ 的 $a,b$。最终,所有满足条件的三元组 $(a,b,c)$ 即为答案。
3. 在 $xy$ 平面内,有 $n$ 条直线,其中任意两条直线不平行,且没有三条直线共点。问这些直线将平面分成了多少个部分。
首先,我们考虑 $n=1,2,3$ 的情况。当 $n=1$ 时,直线将平面分成了 $2$ 个部分;当 $n=2$ 时,直线将平面分成了 $4$ 个部分;当 $n=3$ 时,直线将平面分成了 $7$ 个部分。
接下来,我们考虑 $n$ 增加 $1$ 后,新加入的一条直线将如何改变平面的分割情况。
假设新加入的直线与已有的 $n$ 条直线都不平行,也不共点。那么,新加入的直线将会与已有的 $n$ 条直线相交,将平面分成若干个部分。具体来说,新加入的直线将与已有的 $n$ 条直线产生 $n$ 个交点,将平面分成 $n+1$ 个区域。
但是,我们需要注意到,新加入的直线可能会与已有的某条直线平行,从而不会产生交点。此时,新加入的直线将不会改变平面的分割情况,平面的区域数目仍然为 $f(n)$。因此,我们可以得到递推式:
$$f(n+1)=f(n)+n+1$$
其中,$f(1)=2$。利用递推式,我们可以依次求出 $f(2),f(3),\cdots,f(n)$,最终得到 $f(n)$ 的值。![]()
1. 求解方程:$\sqrt{2x-1}+\sqrt{6-2x}=2$
首先,由于根号内的式子必须非负,所以要求 $2x-1\geq 0$ 和 $6-2x\geq 0$,解得 $x\in[\frac{1}{2},3]$。
接下来,我们可以利用平方的方法来消去根号。将方程两边平方,得到:
$$2x-1+2\sqrt{(2x-1)(6-2x)}+6-2x=4$$
化简一下,得到:
$$\sqrt{(2x-1)(6-2x)}=1$$
再次平方,得到:
$$(2x-1)(6-2x)=1$$
展开化简,得到二次方程:
$$4x^2-16x+13=0$$
利用求根公式,解得:
$$x=2+\frac{\sqrt{3}}{2},2-\frac{\sqrt{3}}{2}$$
但是,我们需要验证这两个解是否满足原方程的定义域。经过计算,我们发现 $2+\frac{\sqrt{3}}{2}otin[\frac{1}{2},3]$,因此舍去,最终的解为 $x=2-\frac{\sqrt{3}}{2}$。
2. 已知 $a,b,c$ 均为正整数,且满足 $a^2+b^2=c^2$,求所有满足 $a+b+c=1000$ 的三元组 $(a,b,c)$。
根据勾股定理,我们可以列出以下条件:
$$\begin{cases}a^2+b^2=c^2\\a+b+c=1000\end{cases}$$
将第二个式子变形,得到:
$$c=1000-a-b$$
代入第一个式子,得到:
$$a^2+b^2=(1000-a-b)^2$$
展开化简,得到:
$$a^2+b^2=10^6-2000a-2000b+2ab$$
移项整理,得到:
$$(a+b-500)^2=250000-c^2$$
因为 $a,b,c$ 均为正整数,所以 $c$ 的取值范围为 $1\leq c<500$。因此,我们只需要枚举 $c$,计算出所有满足条件的 $a,b$ 即可。
具体来说,我们可以枚举 $c$,然后在 $1\leq a+b<1000-c$ 的范围内,计算出所有满足 $(a+b-500)^2=250000-c^2$ 的 $a,b$。最终,所有满足条件的三元组 $(a,b,c)$ 即为答案。
3. 在 $xy$ 平面内,有 $n$ 条直线,其中任意两条直线不平行,且没有三条直线共点。问这些直线将平面分成了多少个部分。
首先,我们考虑 $n=1,2,3$ 的情况。当 $n=1$ 时,直线将平面分成了 $2$ 个部分;当 $n=2$ 时,直线将平面分成了 $4$ 个部分;当 $n=3$ 时,直线将平面分成了 $7$ 个部分。
接下来,我们考虑 $n$ 增加 $1$ 后,新加入的一条直线将如何改变平面的分割情况。
假设新加入的直线与已有的 $n$ 条直线都不平行,也不共点。那么,新加入的直线将会与已有的 $n$ 条直线相交,将平面分成若干个部分。具体来说,新加入的直线将与已有的 $n$ 条直线产生 $n$ 个交点,将平面分成 $n+1$ 个区域。
但是,我们需要注意到,新加入的直线可能会与已有的某条直线平行,从而不会产生交点。此时,新加入的直线将不会改变平面的分割情况,平面的区域数目仍然为 $f(n)$。因此,我们可以得到递推式:
$$f(n+1)=f(n)+n+1$$
其中,$f(1)=2$。利用递推式,我们可以依次求出 $f(2),f(3),\cdots,f(n)$,最终得到 $f(n)$ 的值。
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@bkw.cn 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
推荐视频
- 暂无问答
谁有教育科学出版社高等数学的课后习题答案解析,有的题不会,想看看,谢谢了
baijuxiu·2020-03-12苏教版三年级上册数学评价手册第三单元第四课第二题第25页答案
cengjunsang·2020-03-12数学一题。甲乙两只钟都不准确,甲钟每走24小时快一分钟,乙钟走24小时恰好慢一分钟。
binnongle·2020-03-12北师大版4年级下学期数学知识与能力训练
十六爱人·2020-03-12初中不同底数幂的运算数学题?
binchangcui·2020-03-12人教版五年级下册数学课本134页长方体每个面的长宽高各是多少
baicizhua·2020-03-12求找规律的数学题要比较难的类似这样的
bindaiceng·2020-03-12小学数学教学改革中存在什么问题
几曲屏山·2020-03-17初中数学中考最后几天如何复习
baoshaocui·2020-03-17小学教材二年级下册数学学法大视野答案
cangzhanji·2020-03-21
2018年云南一级建造师资格考试考务工作通知
帮考网校·2018-07-102019年一级建造师《民航机场》历年真题精选
帮考网校·2019-11-022019年一级建造师《港口与航道》章节练习题精选
帮考网校·2019-11-04吉林省2020年一建考试时间已公布!怎么报名?
帮考网校·2020-01-23速看!非全日制学历能报考一级建造师吗?
帮考网校·2019-12-312020年一级建造师《工程经济》每日一练
帮考网校·2020-03-202020年一级建造师《水利工程》历年真题精选
帮考网校·2020-04-022020年一级建造师《机电工程》每日一练0410
帮考网校·2020-04-102020年一级建造师《铁路工程》模拟试题0512
帮考网校·2020-05-122020年一级建造师《建筑工程》模拟试题0522
帮考网校·2020-05-22
- 暂无问答
热门视频
 05:35依法实施计量检定是如何的?
05:35依法实施计量检定是如何的?2023-03-29
 01:18常用机电设备单体试运行及规定的通用规定有哪些?
01:18常用机电设备单体试运行及规定的通用规定有哪些?2023-03-28
 01:13单体试运行的主要范围及目的是什么?
01:13单体试运行的主要范围及目的是什么?2023-03-28
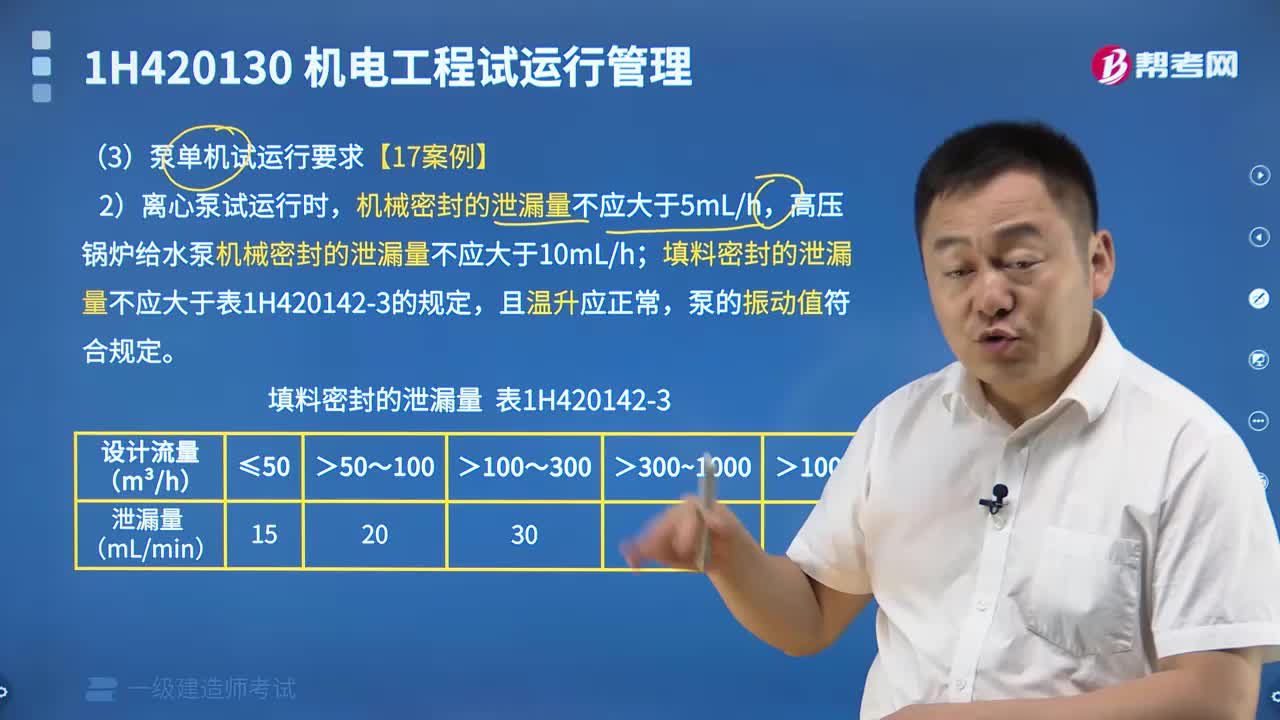 04:14泵单机试运行要求都有什么?
04:14泵单机试运行要求都有什么?2023-03-28
 01:44单体试运行前必须具备的条件有什么?
01:44单体试运行前必须具备的条件有什么?2023-03-28
互动交流

微信扫码关注公众号
获取更多考试热门资料