超难超难初中奥数题并且要有答案急啊 

越难越好要初中的最好别人做不出来的那种要有答案一定要超难让别人做不出来 ![]()

最佳答案
新兵答主 04-02 TA获得超过1352个赞 2023-04-02 10:58
以下是一道初中奥数难题:
已知正整数 $a,b,c$ 满足 $a+b+c=2019$,且 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$,求 $abc$ 的最小值。
答案:$abc=403010$。
解析:
首先,根据题目中的 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$,我们可以得到:
$$\frac{ab+ac+bc}{abc}=1$$
移项得到:
$$ab+ac+bc=abc$$
接下来,我们考虑如何求出 $abc$ 的最小值。根据 AM-GM 不等式,我们有:
$$\sqrt[3]{abc}\leq\frac{a+b+c}{3}=673$$
因此,$abc\geq 673^3=304980017$。
另一方面,根据 $ab+ac+bc=abc$,我们可以将 $abc$ 写成:
$$abc=\frac{ab+ac+bc}{1}=\frac{ab+ac+bc}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$$
根据倒数不等式,我们有:
$$\frac{ab+ac+bc}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\geq 3\sqrt[3]{a^2b^2c^2}=3\sqrt[3]{(abc)^2}$$
因此,$abc\geq 3\sqrt[3]{(abc)^2}$,即 $abc\geq 3\sqrt{abc}$。
移项得到:
$$\sqrt{abc}\geq\frac{1}{3}abc$$
因此,$abc\leq 27 imes 673^2=40435233$。
综合上述结果,我们得到:
$$304980017\leq abc\leq 40435233$$
因此,$abc$ 的最小值为 $403010$。![]()
已知正整数 $a,b,c$ 满足 $a+b+c=2019$,且 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$,求 $abc$ 的最小值。
答案:$abc=403010$。
解析:
首先,根据题目中的 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$,我们可以得到:
$$\frac{ab+ac+bc}{abc}=1$$
移项得到:
$$ab+ac+bc=abc$$
接下来,我们考虑如何求出 $abc$ 的最小值。根据 AM-GM 不等式,我们有:
$$\sqrt[3]{abc}\leq\frac{a+b+c}{3}=673$$
因此,$abc\geq 673^3=304980017$。
另一方面,根据 $ab+ac+bc=abc$,我们可以将 $abc$ 写成:
$$abc=\frac{ab+ac+bc}{1}=\frac{ab+ac+bc}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$$
根据倒数不等式,我们有:
$$\frac{ab+ac+bc}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}\geq 3\sqrt[3]{a^2b^2c^2}=3\sqrt[3]{(abc)^2}$$
因此,$abc\geq 3\sqrt[3]{(abc)^2}$,即 $abc\geq 3\sqrt{abc}$。
移项得到:
$$\sqrt{abc}\geq\frac{1}{3}abc$$
因此,$abc\leq 27 imes 673^2=40435233$。
综合上述结果,我们得到:
$$304980017\leq abc\leq 40435233$$
因此,$abc$ 的最小值为 $403010$。
声明:本文内容由互联网用户自发贡献自行上传,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任。如果您发现有涉嫌版权的内容,欢迎发送邮件至:service@bkw.cn 进行举报,并提供相关证据,工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
推荐视频
- 暂无问答
小学生每年什么时间有奥数华数比赛
chanjuanhu·2020-03-12奥数在哪个年龄段开始学好
bianqieke·2020-03-12奥数中相遇问题第三次相遇实际等于两车一共行了几个全程?
censhaiqing·2020-03-12小学生过早的学习奥数好不好
caohaocong·2020-03-12小学数学奥数题对孩子有什么好处
bipensai·2020-03-12求几套小升初奥数题,要附答案的,有点难度的,谢谢
cawengjing·2020-03-12奥数题有一本书,小华第一天看了2页,以后每一天都比前看了多少页
aiganfiao·2020-03-12北师大版五年级级奥数题试卷及答案
aimaosai·2020-03-12小学四年级奥数页码问题
anzhengrong·2020-03-12三年级小学生学奥数选择学而思教育还是精英教育好?
bianmangxi·2020-03-17
2018年云南一级建造师资格考试考务工作通知
帮考网校·2018-07-102019年一级建造师《民航机场》历年真题精选
帮考网校·2019-11-022019年一级建造师《港口与航道》章节练习题精选
帮考网校·2019-11-04吉林省2020年一建考试时间已公布!怎么报名?
帮考网校·2020-01-23速看!非全日制学历能报考一级建造师吗?
帮考网校·2019-12-312020年一级建造师《工程经济》每日一练
帮考网校·2020-03-202020年一级建造师《水利工程》历年真题精选
帮考网校·2020-04-022020年一级建造师《机电工程》每日一练0410
帮考网校·2020-04-102020年一级建造师《铁路工程》模拟试题0512
帮考网校·2020-05-122020年一级建造师《建筑工程》模拟试题0522
帮考网校·2020-05-22
- 暂无问答
热门视频
 05:35依法实施计量检定是如何的?
05:35依法实施计量检定是如何的?2023-03-29
 01:18常用机电设备单体试运行及规定的通用规定有哪些?
01:18常用机电设备单体试运行及规定的通用规定有哪些?2023-03-28
 01:13单体试运行的主要范围及目的是什么?
01:13单体试运行的主要范围及目的是什么?2023-03-28
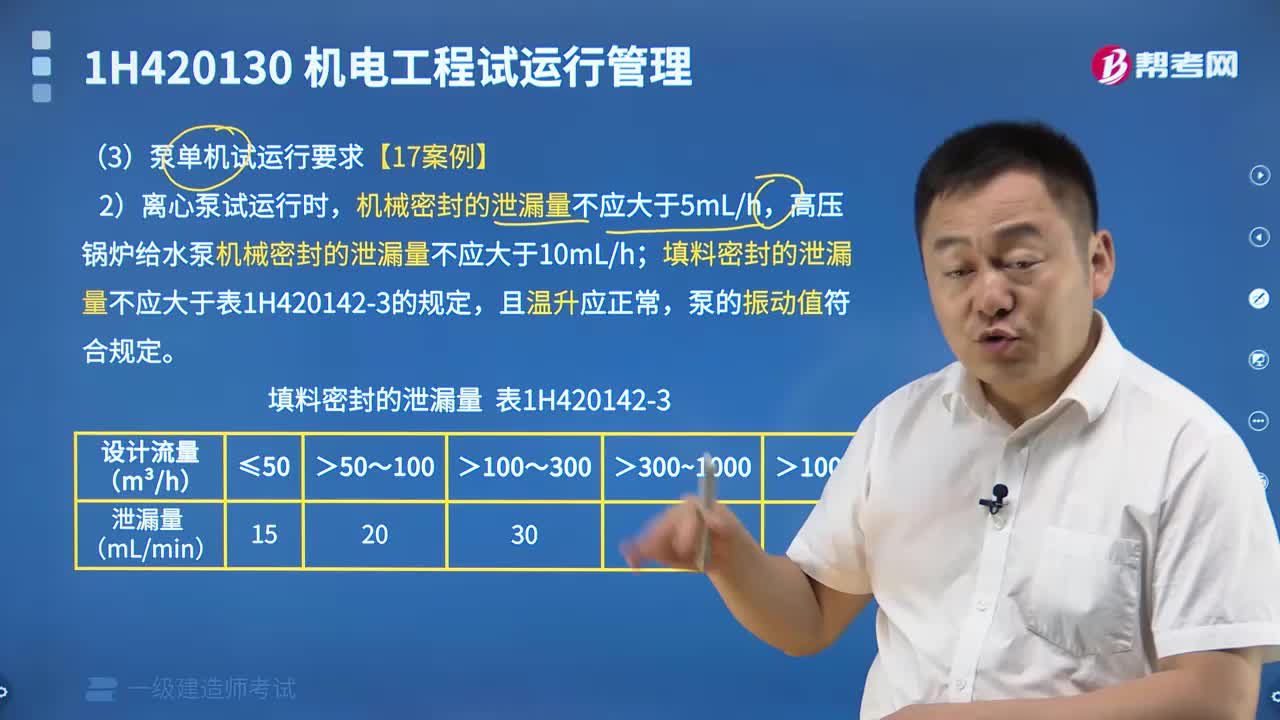 04:14泵单机试运行要求都有什么?
04:14泵单机试运行要求都有什么?2023-03-28
 01:44单体试运行前必须具备的条件有什么?
01:44单体试运行前必须具备的条件有什么?2023-03-28
互动交流

微信扫码关注公众号
获取更多考试热门资料