- 组合型选择题 下列关于回归平方和的说法,正确的有()。 Ⅰ.总的变差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
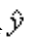 与均值离差
与均值离差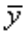 的平方和 Ⅳ.实际值y与均值
的平方和 Ⅳ.实际值y与均值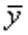 离差的平方和
离差的平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅲ、Ⅳ
- D 、Ⅱ、Ⅲ

扫码下载亿题库
精准题库快速提分
 参考答案
参考答案【正确答案:B】
总的变差平方和(TSS)可以分解为回归平方和(SSR)和残差平方和(ESS)两部分。其中,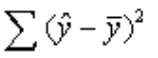 是回归值
是回归值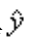 与均值
与均值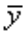 的离差平方和,记为RSS。 RSS反映了TSS中被Y对x回归说明的部分。ESS是TSS中除了Y对X回归之外的一切随机因素构成的部分。三个平方和的关系是TSS=RSS+ESS。
的离差平方和,记为RSS。 RSS反映了TSS中被Y对x回归说明的部分。ESS是TSS中除了Y对X回归之外的一切随机因素构成的部分。三个平方和的关系是TSS=RSS+ESS。
 您可能感兴趣的试题
您可能感兴趣的试题- 1 【组合型选择题】下列关于回归平方和的说法,正确的有()。 Ⅰ.总的变差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值 离差的平方和 Ⅳ.实际值y与均值
离差的平方和 Ⅳ.实际值y与均值 离差的平方和
离差的平方和 - A 、Ⅰ、Ⅱ、Ⅲ
- B 、Ⅰ、Ⅱ、Ⅳ
- C 、Ⅰ、Ⅲ
- D 、Ⅰ、Ⅳ
- 2 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值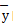 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 3 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值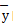 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 4 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值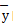 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 5 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值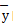 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 6 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值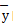 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 7 【组合型选择题】下列关于回归平方和的说法,正确的有( )。 Ⅰ.总的离差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值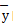 的离差平方和 Ⅳ.实际值y与均值
的离差平方和 Ⅳ.实际值y与均值 的离差平方和
的离差平方和 - A 、Ⅰ、Ⅱ
- B 、Ⅰ、Ⅲ
- C 、Ⅰ、Ⅳ
- D 、Ⅱ、Ⅲ
- 8 【组合型选择题】下列关于回归平方和的说法,正确的有()。 Ⅰ.总的变差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值 离差的平方和 Ⅳ.实际值y与均值
离差的平方和 Ⅳ.实际值y与均值 离差的平方和
离差的平方和 - A 、Ⅰ、Ⅱ、Ⅲ
- B 、Ⅰ、Ⅱ、Ⅳ
- C 、Ⅰ、Ⅲ
- D 、Ⅰ、Ⅳ
- 9 【组合型选择题】下列关于回归平方和的说法,正确的有()。 Ⅰ.总的变差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值 离差的平方和 Ⅳ.实际值y与均值
离差的平方和 Ⅳ.实际值y与均值 离差的平方和
离差的平方和 - A 、Ⅰ、Ⅱ、Ⅲ
- B 、Ⅰ、Ⅱ、Ⅳ
- C 、Ⅰ、Ⅲ
- D 、Ⅰ、Ⅳ
- 10 【组合型选择题】下列关于回归平方和的说法,正确的有()。 Ⅰ.总的变差平方和与残差平方和之差 Ⅱ.无法用回归直线解释的离差平方和 Ⅲ.回归值
 与均值
与均值 离差的平方和 Ⅳ.实际值y与均值
离差的平方和 Ⅳ.实际值y与均值 离差的平方和
离差的平方和 - A 、Ⅰ、Ⅱ、Ⅲ
- B 、Ⅰ、Ⅱ、Ⅳ
- C 、Ⅰ、Ⅲ
- D 、Ⅰ、Ⅳ
热门试题换一换
- 期货市场价格的变动与现货价格的变动之间总是一致的。
- 资产重组常用的评估方法是()。 Ⅰ.资产定价法 Ⅱ.收益现值法 Ⅲ.重置成本法 Ⅳ.市场价值法
- 完全竞争厂商对要素的需求曲线可以用()表示。
- 财政赤字会不会引起通货膨胀,取决于() 。
- “因素模型”也被称为()。 Ⅰ. 指数模型 Ⅱ. 林特纳模型 Ⅲ. 夏普模型 Ⅳ. 费雪模型
- 证券分析师进行证券投资分析的信息来源渠道可以有()。Ⅰ.市场传言Ⅱ.专家访谈 Ⅲ.市场调査Ⅳ.实地考察
- 在经济扩张时,在其他经济变量不变的情况下,利率水平随着收入的增加而()。
- 根据《上市公司行业分类指引》,下列说法正确的是()。
亿题库—让考试变得更简单
已有600万用户下载
 9Zlvp
9Zlvp
