
下载亿题库APP
联系电话:400-660-1360

下载亿题库APP
联系电话:400-660-1360

请谨慎保管和记忆你的密码,以免泄露和丢失

请谨慎保管和记忆你的密码,以免泄露和丢失

2020年MBA考试《数学》考试共25题,分为问题求解和条件充分性判断。小编为您整理第五章 数列5道练习题,附答案解析,供您备考练习。
1、已知等差数列 的公差不为0,但第3、4、7项构成等比数列,
的公差不为0,但第3、4、7项构成等比数列,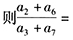 ()。【问题求解】
()。【问题求解】
A.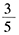
B.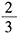
C.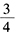
D.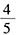
正确答案:A
答案解析:由已知第3、4、7项构成等比数列,即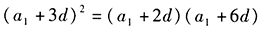 ,化简得
,化简得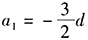 ,
,
因此 。
。
2、三个不相同的非零实数a,b,c成等差数列,又a,c,b恰成等比数列,则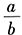 ()。【问题求解】
()。【问题求解】
A.2
B.4
C.-4
D.-2
E.3
正确答案:B
答案解析:a,b,c成等差数列,则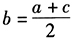 ;a,c,b成等比数列,则有
;a,c,b成等比数列,则有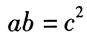 ;
;
由 c=2b-a,得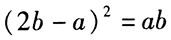 ,整理可知
,整理可知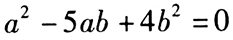 ,即
,即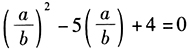 ,解析:得
,解析:得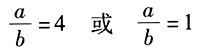 ,因为a≠b,所以
,因为a≠b,所以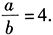
3、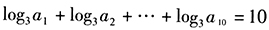 。()
。()
(1)在等比数列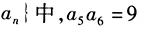
(2)在等比数列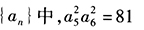 【条件充分性判断】
【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:E
答案解析:取等比数列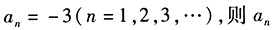 满足条件(1)和条件(2),但题干无意义,从而答案只能选E。
满足条件(1)和条件(2),但题干无意义,从而答案只能选E。
4、已知数列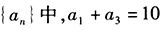 的值一定是1。()
的值一定是1。()
(1)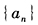 是等差数列,且
是等差数列,且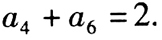
(2)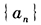 是等比数列,且
是等比数列,且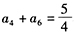 【条件充分性判断】
【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:B
答案解析:由条件(1) ,得公差
,得公差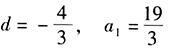 ,
,
从而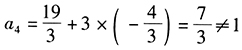 ,
,
即条件(1)不充分。
由条件(2)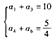 ,设公比为q,则
,设公比为q,则 ,得
,得 ,所以
,所以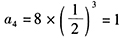 ,即条件(2)充分。
,即条件(2)充分。
5、实数a,b,c成等比数列。()
(1)关于x的一元二次方程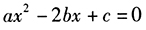 有两个相等实数根
有两个相等实数根
(2)lga,lgb,lgc成等差数列【条件充分性判断】
A.条件(1)充分,但条件(2)不充分
B.条件(2)充分,但条件(1)不充分
C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D.条件(1)充分,条件(2)也充分
E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
正确答案:B
答案解析:题干要求推出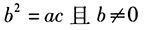 。取a=1,b=c=0,则知条件(1)不充分。
。取a=1,b=c=0,则知条件(1)不充分。
由条件(2)可知a>0,b>O,c>0,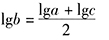 ,因此
,因此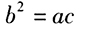 且b≠0,从而条件(2)充分。
且b≠0,从而条件(2)充分。
 05:31
05:312020-05-15
 02:38
02:382020-05-15
 04:04
04:042020-05-15
 03:35
03:352020-05-15
 04:00
04:002020-05-15

微信扫码关注公众号
获取更多考试热门资料