2020年MBA考试《数学》考试共25题，分为问题求解和条件充分性判断。小编为您整理第九章 排列与组合5道练习题，附答案解析，供您备考练习。

1、n=3。（）
（1）若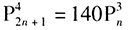
（2）若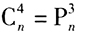【条件充分性判断】

A.条件（1）充分，但条件（2）不充分

B.条件（2）充分，但条件（1）不充分

C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分

D.条件（1）充分，条件（2）也充分

E.条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分

正确答案:A

答案解析:由条件（1），得（2n+1）（2n）（2n-1）（2n-2）=140n（n-1）（n-2），即，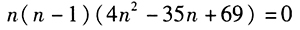
即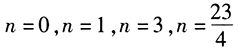，因为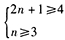且n为整数，所以n=3，即条件（1）是充分的。
由条件（2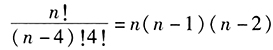），可得 n（n-1）（n-2）（n-3）=24n（n-1）（n-2），整理得：n（n-1）（n-2）（n-3-24）=0，即 n=0，n=1，n=2，n=27。由于n≥4，从而n=27，条件（2）不充分。

2、有4名男生，3名女生站成一排，男生不站排头和排尾的排法种数是（）。【问题求解】

A.760

B.720

C.680

D.620

E.480

正确答案:B

答案解析:第一个步骤，选1名女生站排头，共有3种可能性；
第二个步骤，再选1名女生站排尾，则有2种可能性；
第三个步骤，诖剩下5人站位，则有5！=120（种）可能性；
从而总排法为3×2×120=720（种）。

3、10产品中有3件次品，现从中任意抽出4件检验，其中至少有2件次品的抽法种数是（）。【问题求解】

A.120

B.116

C.98

D.86

E.70

正确答案:E

答案解析:2件次品2件正品的取法为
3件次品1件正品的取法为
从而总取法为63+7=70（种）。

4、从5名女生、4名男生中选出3人参加数学竞赛，则选出的3人中至少有一名女生的选法共有（）种。【问题求解】

A.80

B.76

C.70

D.64

E.60

正确答案:A

答案解析:总选法为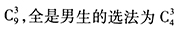从而至少有二名女生的选法为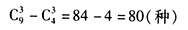

5、N=1260。（）
（1）有实验员9人，分成3组，分别为2，3，4人，去进行内容相同的实验，共有N种不同的分法
（2）有实验员9人，分成3组，分别为2，3，4人，去进行内容不同的实验，共有N种不同的分法【条件充分性判断】

A.条件（1）充分，但条件（2）不充分

B.条件（2）充分，但条件（1）不充分

C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分

D.条件（1）充分，条件（2）也充分

E.条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分

正确答案:A

答案解析:由条件（1），即条件（1）是充分的。
由条件（2），即条件（2）不充分。